The Ridge Backtest Metric: Backtesting Expected Shortfall

Challenges with backtesting Expected Shortfall

Recent regulations are increasingly moving toward the use of Expected Shortfall (ES) as a measure to capture risk. Although ES fixes many issues with VaR, there are challenges when it comes to backtesting.

Although VaR has been widely-used for decades, its shortcomings have prompted the switch to ES. Firstly, as a percentile measure, VaR does not adequately capture tail risk. Unlike VaR, which gives the maximum expected portfolio loss in a given time period and at a specific confidence level, ES gives the average of all potential losses greater than VaR (see figure 1). Consequently, unlike Var, ES can capture a range of tail scenarios. Secondly, VaR is not sub-additive. ES, however, is sub-additive, which makes it better at accounting for diversification and performing attribution. As such, more recent regulation, such as FRTB, is replacing the use of VaR with ES as a risk measure.

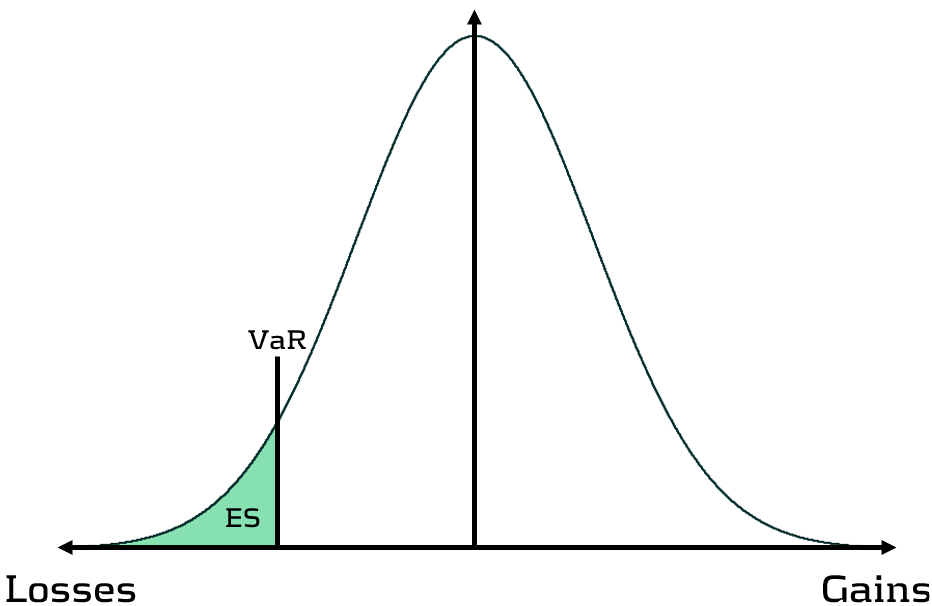
Figure 1: Comparison of VaR and ES

Elicitability is a necessary mathematical condition for backtestability. As ES is non-elicitable, unlike VaR, ES backtesting methods have been a topic of debate for over a decade. Backtesting and validating ES estimates is problematic – how can a daily ES estimate, which is a function of a probability distribution, be compared with a realised loss, which is a single loss from within that distribution? Many existing attempts at backtesting have relied on approximations of ES, which inevitably introduces error into the calculations.

The three main issues with ES backtesting can be summarised as follows:

1. Transparency
   • Without reliable techniques for backtesting ES, banks struggle to have transparency on the performance of their models. This is particularly problematic for regulatory compliance, such as FRTB.
2. Sensitivity
   • Existing VaR and ES backtesting techniques are not sensitive to the magnitude of the overages. Instead, these techniques, such as the Traffic Light Test (TLT), only consider the frequency of overages that occur.
3. Stability
   • As ES is conditional on VaR, any errors in VaR calculation lead to errors in ES. Many existing ES backtesting methodologies are highly sensitive to errors in the underlying VaR calculations.

Ridge Backtesting: A solution to ES backtesting

One often-cited solution to the ES backtesting problem is the ridge backtesting approach. This method allows non-elicitable functions, such as ES, to be backtested in a manner that is stable with regards to errors in the underlying VaR estimations. Unlike traditional VaR backtesting methods, it is also sensitive to the magnitude of the overages and not just their frequency.

The ridge backtesting test statistic is defined as:

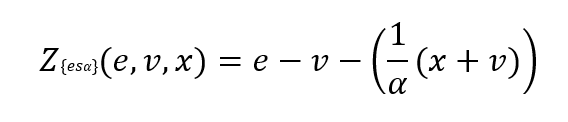
where 𝑣 is the VaR estimation, 𝑒 is the expected shortfall prediction, 𝑥 is the portfolio loss and 𝛼 is the confidence level for the VaR estimation.

The value of the ridge backtesting test statistic provides information on whether the model is over or underpredicting the ES. The technique also allows for two types of backtesting; absolute and relative. Absolute backtesting is denominated in monetary terms and describes the absolute error between predicted and realised ES. Relative backtesting is dimensionless and describes the relative error between predicted and realised ES. This can be particularly useful when comparing the ES of multiple portfolios. The ridge backtesting result can be mapped to the existing Basel TLT RAG zones, enabling efficient integration into existing risk frameworks.

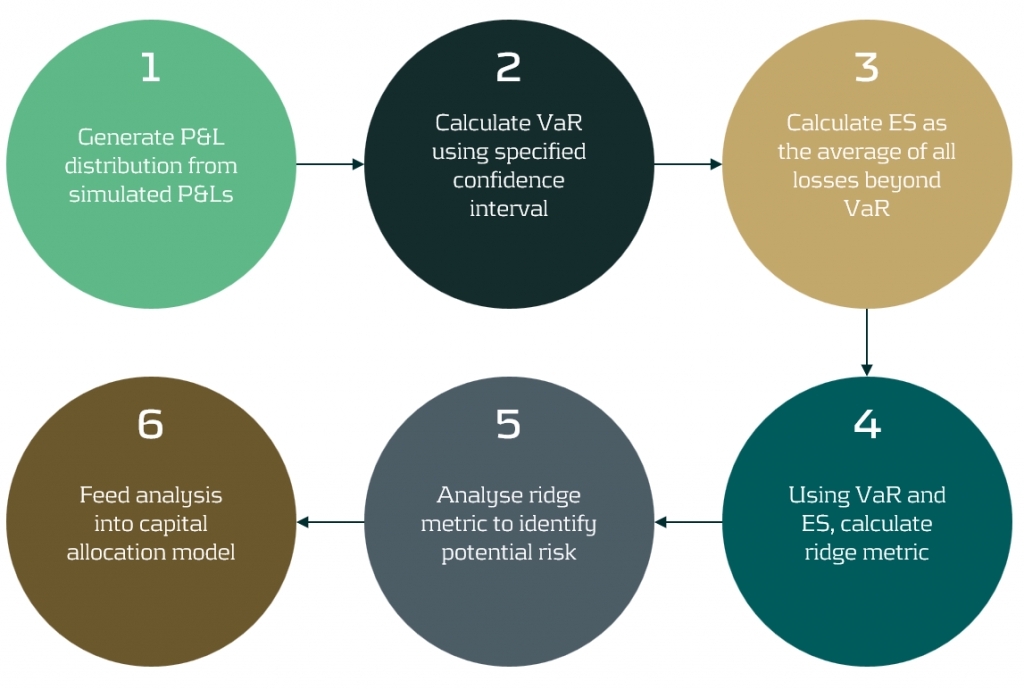
Figure 2: The ridge backtesting methodology

Sensitivity to Overage Magnitude

Unlike VaR backtesting, which does not distinguish between overages of different magnitudes, a major advantage of ES ridge backtesting is that it is sensitive to the size of each overage. This allows for better risk management as it identifies periods with large overages and also periods with high frequency of overages.

Below, in figure 3, we demonstrate the effectiveness of the ridge backtest by comparing it against a traditional VaR backtest. A scenario was constructed with P&Ls sampled from a Normal distribution, from which a 1-year 99% VaR and ES were computed. The sensitivity of ridge backtesting to overage magnitude is demonstrated by applying a range of scaling factors, increasing the size of overages by factors of 1, 2 and 3. The results show that unlike the traditional TLT, which is sensitive only to overage frequency, the ridge backtesting technique is effective at identifying both the frequency and magnitude of tail events. This enables risk managers to react more quickly to volatile markets, regime changes and mismodelling of their risk models.

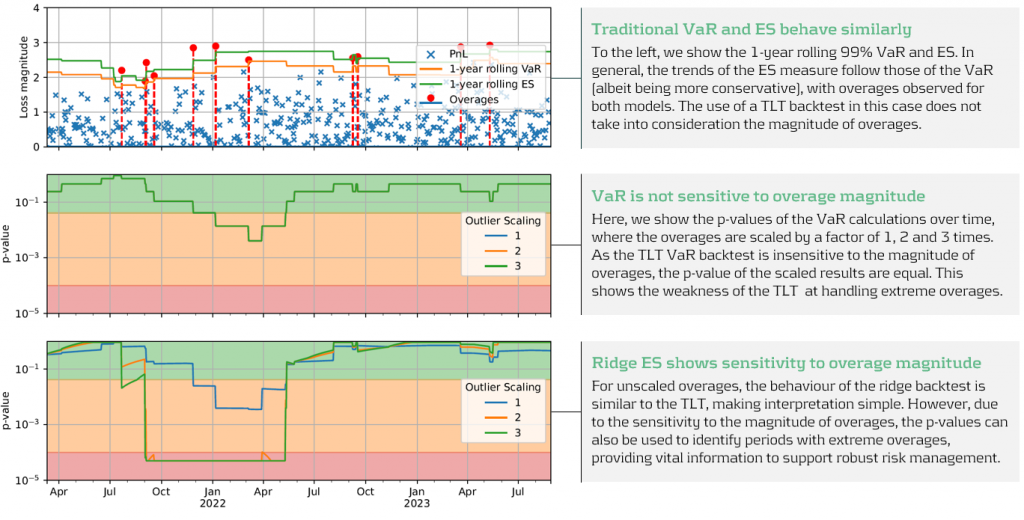
Figure 3: Demonstration of ridge backtesting’s sensitivity to overage magnitude.

The Benefits of Ridge Backtesting

Rapidly changing regulation and market regimes require banks enhance their risk management capabilities to be more reactive and robust. In addition to being a robust method for backtesting ES, ridge backtesting provides several other benefits over alternative backtesting techniques, providing banks with metrics that are sensitive and stable.

Despite the introduction of ES as a regulatory requirement for banks choosing the internal models approach (IMA), regulators currently do not require banks to backtest their ES models. This leaves a gap in banks’ risk management frameworks, highlighting the necessity for a reliable ES backtesting technique. Despite this, banks are being driven to implement ES backtesting methodologies to be compliant with future regulation and to strengthen their risk management frameworks to develop a comprehensive understanding of their risk.

Ridge backtesting gives banks transparency to the performance of their ES models and a greater reactivity to extreme events. It provides increased sensitivity over existing backtesting methodologies, providing information on both overage frequency and magnitude. The method also exhibits stability to any underlying VaR mismodelling.

In figure 4 below, we summarise the three major benefits of ridge backtesting.

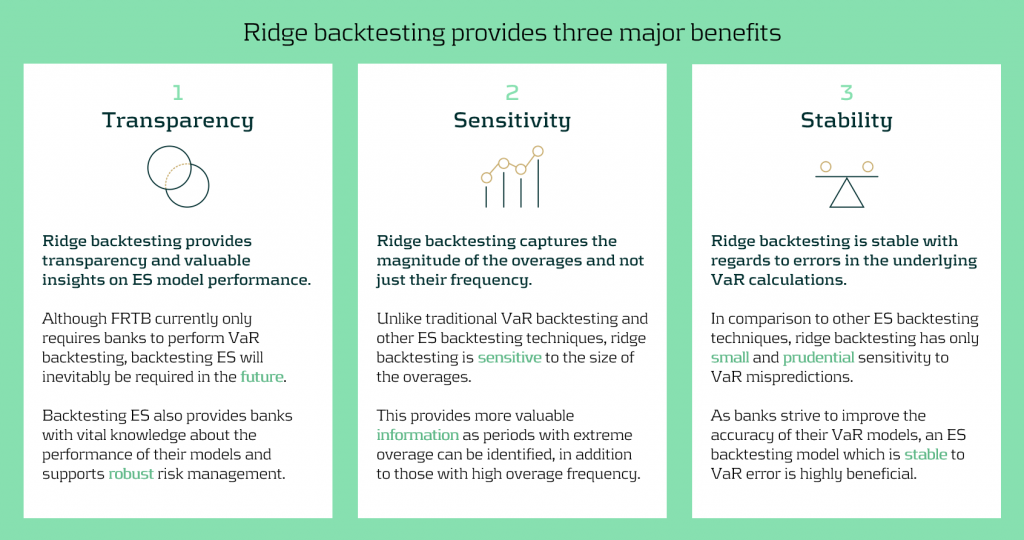
Figure 4: The three major benefits of ridge backtesting.

Conclusion

The lack of regulatory control and guidance on backtesting ES is an obvious concern for both regulators and banks. Failure to backtest their ES models means that banks are not able to accurately monitor the reliability of their ES estimates. Although the complexities of backtesting ES has been a topic of ongoing debate, we have shown in this article that ridge backtesting provides a robust and informative solution. As it is sensitive to the magnitude of overages, it provides a clear benefit in comparison to traditional VaR TLT backtests that are only sensitive to overage frequency. Although it is not a regulatory requirement, regulators are starting to discuss and recommend ES backtesting. For example, the PRA, EBA and FED have all recommended ES backtesting in some of their latest publications. However, despite the fact that regulation currently only requires banks to perform VaR backtesting, banks should strive to implement ES backtesting as it supports better risk management.

For more information on this topic, contact Dilbagh Kalsi (Partner) or Hardial Kalsi (Manager).