In brief
- Prepayment modelling can help institutions successfully prepare for and navigate a rise in prepayments due to changes in the financial landscape.
- Two important prepayment modelling types are highlighted and compared: logistic regression vs Cox Proportional Hazard.
- Although the Cox Proportional Hazard model is theoretically preferred under specific conditions, the logical regression is preferred in practice under many scenarios.
The borrowers' option to prepay on their loan induces uncertainty for lenders. How can lenders protect themselves against this uncertainty? Various prepayment modelling approaches can be selected, with option risk and survival analyses being the main alternatives under discussion.
Prepayment options in financial products spell danger for institutions. They inject uncertainty into mortgage portfolios and threaten fixed-rate products with volatile cashflows. To safeguard against losses and stabilize income, institutions must master precise prepayment modelling.
This article delves into the nuances and options regarding the modelling of mortgage prepayments (a cornerstone of Asset Liability Management (ALM)) with a specific focus on survival models.
Understanding the influences on prepayment dynamics
Prepayments are triggered by a range of factors – everything from refinancing opportunities to life changes, such as selling a house due to divorce or moving. These motivations can be grouped into three overarching categories: refinancing factors, macroeconomic factors, and loan-specific factors.
- Refinancing factors
This encompasses key financial drivers (such as interest rates, mortgage rates and penalties) and loan-specific information (including interest rate reset dates and the interest rate differential for the customer). Additionally, the historical momentum of rates and the steepness of the yield curve play crucial roles in shaping refinancing motivations.
- Macro-economic factors
The overall state of the economy and the conditions of the housing market are pivotal forces on a borrower's inclination to exercise prepayment options. Furthermore, seasonality adds another layer of variability, with prepayments being notably higher in certain months. For example, in December, when clients have additional funds due to payment of year-end bonusses and holiday budgets.
- Loan-specific factors
The age of the mortgage, type of mortgage, and the nature of the property all contribute to prepayment behavior. The seasoning effect, where the probability of prepayment increases with the age of the mortgage, stands out as a paramount factor.
These factors intricately weave together, shaping the landscape in which customers make decisions regarding prepayments. Prepayment modelling plays a vital role in helping institutions to predict the impact of these factors on prepayment behavior.
The evolution of prepayment modelling
Research on prepayment modelling originated in the 1980s and initially centered around option-theoretic models that assume rational customer behavior. Over time, empirical models that cater for customer irrationality have emerged and gained prominence. These models aim to capture the more nuanced behavior of customers by explaining the relationship between prepayment rates and various other factors. In this article, we highlight two important types of prepayment models: logistic regression and Cox Proportional Hazard (Survival Model).
Logistic regression
Logistic regression, specifically its logit or probit variant, is widely employed in prepayment analysis. This is largely because it caters for the binary nature of the dependent variable indicating the occurrence of prepayment events and it moreover flexible. That is, the model can incorporate mortgage-specific and overall economic factors as regressors and can handle time-varying factors and a mix of continuous and categorical variables.
Once the logistic regression model is fitted to historical data, its application involves inputting the characteristics of a new mortgage and relevant economic factors. The model’s output provides the probability of the mortgage undergoing prepayment. This approach is already prevalent in banking practices, and frequently employed in areas such as default modeling and credit scoring. Consequently, it’s favored by many practitioners for prepayment modeling.
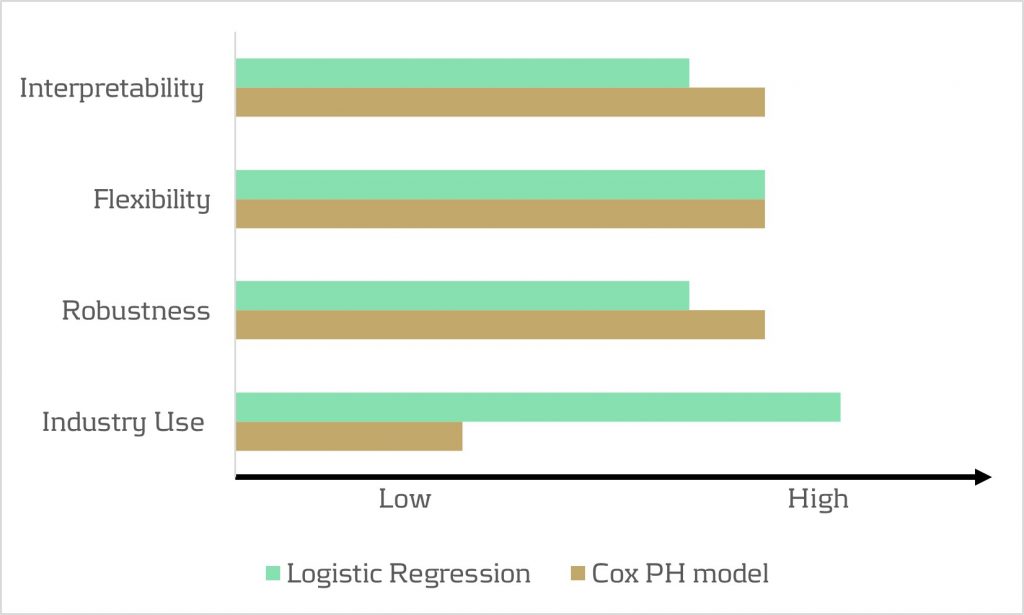
Despite its widespread use, the model has drawbacks. While its familiarity in banking scenarios offers simplicity in implementation, it lacks the interpretability characteristic of the Proportional Hazard model discussed below. Furthermore, in terms of robustness, a minimal drawback is that any month-on-month change in results can be caused by numerous factors, which all affect each other.
Cox Proportional Hazard (Survival model)
The Cox Proportional Hazard (PH) model, developed by Sir David Cox in 1972, is one of the most popular models in survival analysis. It consists of two core parts:
- Survival time. With the Cox PH model, the variable of interest is the time to event. As the model stems from medical sciences, this event is typically defined as death. The time variable is referred to as survival time because it’s the time a subject has survived over some follow-up period.
- Hazard rate. This is the distribution of the survival time and is used to predict the probability of the event occurring in the next small-time interval, given that the event has not occurred beforehand. This hazard rate is modelled based on the baseline hazard (the time development of the hazard rate of an average patient) and a multiplier (the effect of patient-specific variables, such as age and gender). An important property of the model is that the baseline hazard is an unspecified function.
To explain how this works in the context of prepayment modelling for mortgages:
- The event of interest is the prepayment of a mortgage.
- The hazard rate is the probability of a prepayment occurring in the next month, given that the mortgage has not been prepaid beforehand. Since the model estimates hazard rates of individual mortgages, it’s modelled using loan-level data.
- The baseline hazard is the typical prepayment behavior of a mortgage over time and captures the seasoning effect of the mortgage.
- The multiplier of the hazard rate is based on mortgage-specific variables, such as the interest rate differential and seasonality.
For full prepayments, where the mortgage is terminated after the event, the Cox PH model applies in its primary format. However, partial prepayments (where the event is recurring) require an extended version, known as the recurrent event PH model. As a result, when using the Cox PH model, , the modelling of partial and full prepayments should be conducted separately, using slightly different models.
The attractiveness of the Cox PH model is due to several features:
- The interpretability of the model. The model makes it possible to quantify the influence of various factors on the likelihood of prepayment in an intuitive way.
- The flexibility of the model. The model offers the flexibility to handle time-varying factors and a mix of continuous and categorical variables, as well as the ability to incorporate recurrent events.
- The multiplier means the hazard rate can’t be negative. The exponential nature of mortgage-specific variables ensures non-negative estimated hazard rates.
Despite the advantages listed above presenting a compelling theoretical case for using the Cox PH model, it faces limited adoption in practical prepayment modelling by banks. This is primarily due to its perceived complexity and unfamiliarity. In addition, when loan-level data is unavailable, the Cox PH model is no longer an option for prepayment modeling.
Logistic regression vs Cox Proportional Hazard
In scenarios with individual survival time data and censored observations, the Cox PH model is theoretically preferred over logistic regression. This preference arises because the Cox PH model leverages this additional information, whereas logistic regression focuses solely on binary outcomes, disregarding survival time and censoring.
However, practical considerations also come into play. Research shows that in certain cases, the logistic regression model closely approximates the results of the Cox PH model, particularly when hazard rates are low. Given that prepayments in the Netherlands are around 3-10% and associated hazard rates tend to be low, the performance gap between logistic regression and the Cox PH model is minimal in practice for this application. Also, the necessity to create a different PH model for full and partial prepayment adds an additional burden on ALM teams.
In conclusion, when faced with the absence of loan-level data, the logistic regression model emerges as a pragmatic choice for prepayment modeling. Despite the theoretical preference for the Cox PH model under specific conditions, the real-world performance similarities, coupled with the familiarity and simplicity of logistic regression, provide a practical advantage in many scenarios.
How can Zanders support?
Zanders is a thought leader on IRRBB-related topics. We enable banks to achieve both regulatory compliance and strategic risk goals by offering support from strategy to implementation. This includes risk identification, formulating a risk strategy, setting up an IRRBB governance and framework, and policy or risk appetite statements. Moreover, we have an extensive track record in IRRBB and behavioral models such as prepayment models, hedging strategies, and calculating risk metrics, both from model development and model validation perspectives.
Are you interested in IRRBB-related topics such as prepayments? Contact Jaap Karelse, Erik Vijlbrief, Petra van Meel (Netherlands, Belgium and Nordic countries) or Martijn Wycisk (DACH region) for more information.