In this article, we introduce SAC liquidity planning solution focusing on its integrated and predictive planning capabilities. We explain the concerns of corporate treasuries that have invested heavily in SAP BPC (either as standalone instance or embedded on S/4 HANA) and discuss the business case for SAC under different scenarios of extending the BPC planning solution to SAC.
What is SAC?
SAC is the analytics and planning solution within SAP Business Technology Platform which brings together analytics and planning with unique integration to SAP applications and smooth access to heterogeneous data sources.
Among the key benefits of SAC are Extended Planning & Analysis (xP&A) and Predictive Planning based on machine learning models. While xP&A integrates (traditional) financial and operational planning resulting in one connected plan that also meets the needs of operational departments, predictive planning augments decision making through embedded AI & ML capabilities.
Extended Planning & Analysis (xP&A)
Historically, the corporate planning has been typically biased towards finance and it was quite inadequate for operational departments who have to resort to local planning in silos for their own decision making. The xP&A approach goes beyond finance and integrates strategic, financial and operational planning in one connected plan. Planning under xP&A also moves beyond budgeting and rolling forecasts to a more agile and collaborative planning process which is near real-time with faster reaction times.
SAC can be seen as the technology enabler for xP&A, as follows:
- It brings together financial, supply chain, and workforce planning in one connected plan deployed in the cloud;
- Unified planning content with a single version of the truth that everyone is working on (plans are fit for purpose for the individual departments and at the same time integrated into one connected plan);
- Predictive AI and ML models enables more realistic forecasts and facilitate near real-time planning & forecasting;
- Smart analytics features like scenario planning prepare for contingencies and quick reaction;
- SAC integrates with a wide range of data sources like S/4HANA , SuccessFactors, SAP IBP, Salesforce etc.
Predictive Planning
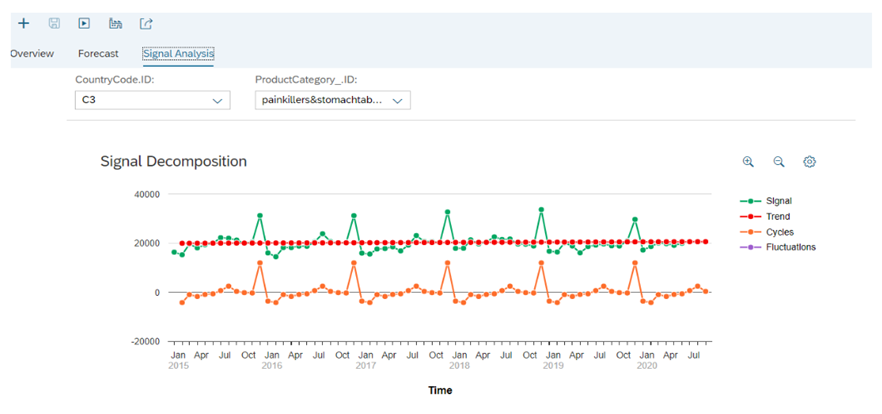
SAC Predictive planning model produces forecasts based on time series. The model is trained with historic data where a statistical algorithm will learn from the data set, i.e. find trends, seasonal variations and fluctuations that characterize the target variable. Upon completion of training, the model produces the forecast as the detailed time series chart for each segment.
In addition to using historical costs to make a prediction, influencer variables can be used to improve the predictive forecasts. Some examples of influencers are energy price when forecasting the energy cost, weather on the day and workday/weekend classification when forecasting daily bike hires.
Influencers are part of the data set and when included in the forecasting model, they contribute towards determining the ‘trend’. They improve the predictive forecasts which can be measured by drop in MAPE (Mean Absolute Percentage Error) and a smaller confidence interval (difference between the Error Max and the Error Min).
Business cases for extension of SAP BPC to SAC
While it may be easier to evaluate the benefits of SAC in a greenfield implementation, it could be challenging to create a suitable business case for customers already using SAP BPC, either standalone or embedded, and interesting to understand how they can preserve their existing assets in a brownfield implementation.
Below we have provided the business case for the 3 planning scenarios for extending the BPC planning to SAC:
Figure: Decomposition of forecast into trend, cycle and fluctuation (left out after trend and cycle are extracted)
Scenario 1: Move planning use cases from BPC to SAC
The ‘Move’ scenario involves re-creation of planning models in SAC. Some of the existing work can be leveraged on; for example, a planning model in SAC can be built through a query coming out of SAP BPC which re-creates the planning dimensions with all their hierarchies. The planning scenarios require more effort as the planning use cases are realized in a different way in SAC than BPC. Functionalities such as disaggregations, version management and simulation are also conceptually different in SAC (compared to BPC).
Note: The re-creation of planning models in SAC through queries from BPC are more relevant for the embedded BPC model, running on SAP BW belonging to S/4 HANA NetWeaver. The integration under a standalone BPC model (using a standalone SAP BW) may not be supported and should be investigated with the vendor.
The key value drivers for this scenario include all the benefits of SAC, such as predictive planning and machine learning, xP&A, modern UX and smart analytics. SAC features on version control, real-time data analysis, lower maintenance cost and faster performance are also possible in the SAP BPC embedded model (advantages over BPC standalone model only).
Scenario 2: Complement existing BPC planning with SAC as planning UX
Here, SAC is used as a tool for entering planning data and data analysis. Data entered in SAC (e.g. via data entry form) is persisted directly in the SAP BPC planning model. LIVE planning is supported only in SAP BPC embedded model (one of the benefits of BPC embedded over standalone).
The key value drivers for this scenario are modern UX and smart analytics (from the firstt scenario), while the functional plans are maintained in BPC.
Scenario 3: Extend BPC with SAC for new functional plans
In this scenario, new functional planning is done in SAC on top of BPC, data is stored in both systems and replicated in both directions.
Key value drivers for this scenario are predictive planning and xP&A (to some extent). A specific use case for the first one is where planning data is brought into SAC, predictive forecasting applied on top of the planned data together with any manual adjustments and data is replicated back to BPC. A use case for the second one is where financial planning done in BPC is integrated with the operational planning done exclusively in SAC.
In conclusion
SAC can be seen as SAP’s vision for Extensible Planning & Analysis (xP&A) as it unifies planning across multiple lines of business while ensuring that plans are meaningful and can be put to action. The predictive time series, AI and ML based models of SAC are key enablers for a near real-time and driver-based planning.
For customers already using BPC (standalone or embedded on S/4 HANA) there are possibilities to complement the existing planning process through SAC. However, to exploit the full benefits in xP&A, it is important to understand the integrated planning approach of SAC which is conceptually different from BPC. While the immediate requirement in a BPC complement scenario could be to realize the current use cases in SAC (in a different way), it makes sense to maintain a strategic outlook, e.g. when creating the planning models in SAC, to achieve the full transformation in future.
References:
Top 10 reasons to move from SAP Business Planning and Consolidation to SAP Analytics Cloud
White-Paper-Extended-Planning-and-Analysis-2022.pdf (fpa-trends.com)
Extended Planning and Analysis | xP&A (sap.com)
SAP Analytics Cloud | BI, Planning, and Predictive Analysis Tools
Hands-On Tutorial: Predictive Planning | SAP Blogs
Predictive Planning – How to use influencers | SAP Blogs
SAP BPC Move to SAC: Benefits & Scenarios of moving SAP BPC planning scenarios to SAP Analytics Cloud | SAP Blogs
Financial planning : SAP Analytics Cloud to replace SAP Business Planning & Consolidation ? | SAP Blogs
Complement Your SAP Business Planning and Consolidation with SAP Analytics Cloud | SAP Blogs
SAP Business Planning & Consolidation for S/4HANA – In a Nutshell | SAP Blogs