Blog
EBA’s Revised Definition of Default
On July 2nd, the European Banking Authority (EBA) published a Consultation Paper proposing amendments to its 2016 Guidelines on the application of the definition of default (DoD). As part of the
Find out more
Recovery and resolution plans have emerged as a key supervisory tool since the global financial crisis.
Solvent wind-down (SWD) is regulated by the European Bank Recovery and Resolution Directive (BRRD) and supervised by the Single Resolution Board (SRB). Banks must demonstrate, by means of an SWD plan that they can exit their trading activities in an orderly manner while avoiding posing risks to the stability of the financial system. The SWD guidance1 sets out the necessary steps and initiatives for banks to take, structured along seven dimensions2 from the Expectations for Banks publication3, to ensure they are resolvable and to demonstrate their preparedness for a potential resolution.
Banks with material trading books4 are expected to develop a granular plan to prove their capability to wind-down their trading books. Winding down trading books requires careful planning and analytical capabilities, including:
The SWD plan outlines the technical aspects of winding down the trading book while the SWD playbook describes the process of how to execute the exit strategy. Banks are expected to initially provide the day-one requirements for the SWD plan and playbook. Thereafter, the SWD plan and playbook need to be expanded and improved to meet the steady-state requirements. This entails a comprehensive upgrade, providing a more granular analysis and the ability to update the exit strategies based on the latest balance sheet within five working days. Note that the bank management could decide to wind down only a few desks. The SWD plan could therefore include multiple scenarios in which different parts of the trading book are wound down.
By 2021, all G-SIBs received instructions from the SRB to work on SWD planning as a Resolution Planning Cycle (RPC) 2022 priority. Other banks have been identified and approached by the SRB in the course of 2022 following a further assessment of the significance of their trading books, to work on SWD planning as an RPC 2023 priority.
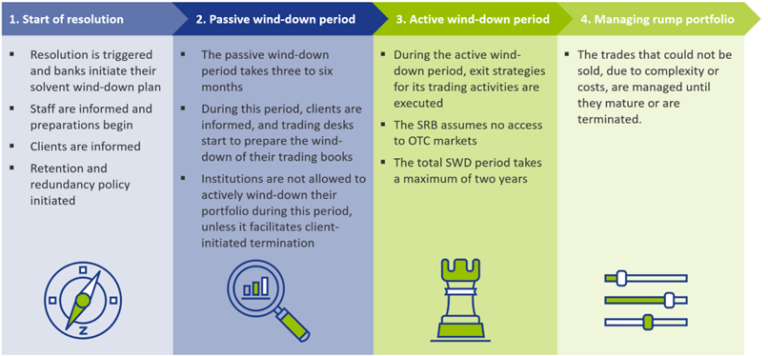
When resolution is triggered, the bank must execute its SWD plan which consists of the four phases indicated in Figure 1. During the first phase, staff and clients are informed and the SWD plan is updated based on the latest trading book status. Then, during the passive wind-down period, trading desks start the preparations to wind down their trading books. During this period, no active trading is allowed, unless specifically requested by the client. During the active wind-down period, exit strategies are executed, while not being able to access the over-the-counter (OTC) market. The bank is required to update their sensitivities (Greeks), costs of winding down, operational costs, and impact on liquidity and RWAs on a quarterly frequency for the full wind-down period. Finally, after two years, most of the trading activities should have been wound down and the few remaining trades that could not be sold, are managed until they mature or are terminated.
Creating a streamlined process to update the SWD plan
One of the larger challenges is to create a streamlined process that enables an update of all exposures and exit strategies for the entire trading book within five working days, which is a steady-state requirement. Since information is usually gathered from various data sources, it can be difficult to update the SWD plan in a timely manner. Therefore, smart tooling should be developed that can assign exit strategies and priorities to certain types of trades to plan the unwinding in the two-year window.
Winding down complex books
Banks with complex or structured books, with positions falling under level 3 of the IFRS13 accounting standards7, could face difficulties unwinding these positions (from a process or cost perspective). These more complex products are usually less liquid, because inputs required to determine the market value are unobservable (by definition, or for example due to low market activity). Banks should provide evidence that they are aware of this complexity and should be able to come up with a reasonable estimate of the costs of unwinding, for example by using the bid/offer spread (if available) and a haircut.
No access to the OTC markets for hedging purposes
One of the assumptions set by the SRB is that the bank has failed to maintain, establish, or re-establish market confidence. Under this assumption, banks cannot continue using the bilateral OTC markets. Consequently, only listed products can be used for hedging purposes. This could result in imperfect hedges and possibly higher exit costs when selling or auctioning trades (please note that trades are often auctioned in groups, i.e. auction packages are created). Additionally, a bank must show how it expects the exit and risk-based costs to evolve during the solvent wind-down period, taking into consideration the changes in the composition of its trading book. To tackle the above two challenges, banks could find ‘natural’ hedges with offsetting risks in the trading books to reduce the risk sensitivity of auction packages. Packages with lower risks are expected to have lower exit costs. In turn, the bank can calculate the exit and risk-based costs for each package in each quarter of the active wind-down phase.
Measuring the impact on RWAs for market risk
Banks are expected to include the potential impact of winding down their portfolios on sensitivities, costs (exit, risk-based and operational), liquidity and RWAs (for market, credit and operational risks) in the SWD plan. This impact analysis must be presented, at least quarterly, during the two-year wind-down period. To measure the impact on the RWAs for market risk, banks are challenged to add the hedges that they want to use during the resolution period in their system. Subsequently, banks should be able to age their portfolio: i.e. banks need to calculate the impact of maturing, terminating, and auctioning of trades in their trading books during the entire wind-down period. If this functionality is not readily available, banks may need to use an alternative method to determine the impact. A possibility to tackle this challenge is to create ‘test’ books, which include listed/cleared trades that will be used for hedging purposes during the active wind-down period.
Liquidity gaps
Finally, the SWD plan should contain an analysis of the impact on liquidity. As banks are in resolution, major cash shortfalls could occur. A thorough analysis of outflows and inflows is necessary to identify potential future cash flow mismatches. One important assumption is that the bank in resolution will lose its investment grade or experience a downgrade of its credit rating, likely resulting in significant collateral/margin calls and potentially creating liquidity gaps. These gaps need to be identified and explained. Banks could prioritize the auction/novation of trades with credit support annexes (CSAs) that have high collateral requirements to close the CSA and free up capital.
Over time, the SRB is likely to amend the guidance on SWD of trading books. The most recent publication date (at the time of writing) is December 2021. We expect that more granular reporting will be required in the future. Additionally, we expect that banks will be required to perform stress testing on their trading books, which may be challenging to incorporate. Nonetheless, no changes to the guidance are expected in 2023.
Creating a solvent wind-down strategy can be very complex and introduce many challenges to banks. A large variety of trading books, interdependencies between trading desks and departments, and a diverse data landscape can all provide difficulties to develop a streamlined process.
The development of a strong SWD plan and playbook can help to tackle these challenges. On top of that, a strong SWD plan also gives a more detailed insight into the activities conducted by the various trading desks as risks and returns of the different trading activities are analyzed. The clear trade-off between risk and return could therefore also be used for strategic decision-making such as:
In the course of 2022, Zanders successfully helped one of the Global Systemically Important Banks (G-SIBs) with the development of a SWD plan and SWD playbook. After working on the day-one requirements, extensive time and effort was spent on optimizing the wind-down process to meet the steady-state requirements. Our support was provided on the points shown in Figure 2.
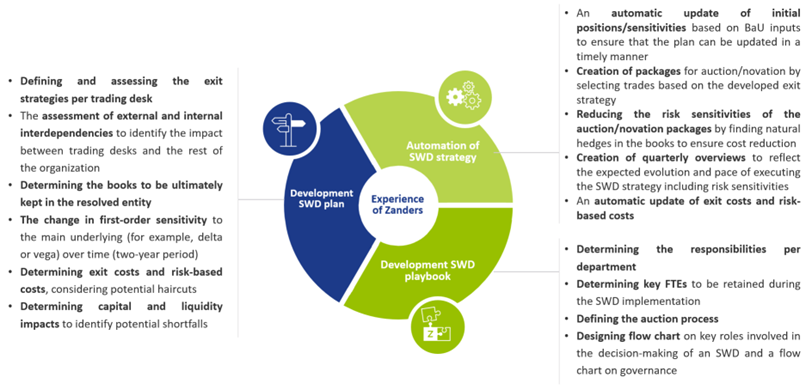
Figure 2: Support provided by Zanders on SWD of trading books.
With our experience across all aspects of the solvent wind-down requirements, we can help you to comply with this regulation. For questions or more information on solvent wind-downs, do not hesitate to contact Jaap Stolp or Ilse Schepers via +31 88 991 02 00.
[1] Latest guidance on SWD of trading books published by the SRB: 2021-12-01_Solvent-wind-down-guidance-for-banks.pdf (europa.eu)
[2] The seven dimensions for assessing resolvability include governance, loss absorbing and recapitalization capacity, liquidity and funding in resolution, operational continuity and access to Financial Market Infrastructure (FMI) services, information systems and data requirements, communication, and separability and restructuring. These dimensions describe the steps banks are expected to take to become resolvable.
[3] The Expectations for Banks by the SRB: EXPECTATIONS FOR BANKS (europa.eu)
[4] The SRB will define banks with material trading books based on, for example, exposures and the complexity of the books.
[5] The SRB encourages banks to provide information on a granular level. Banks should aim for the desk level. However, banks are also allowed to apply a different segmentation if this is more appropriate. For example, a business unit level is allowed if banks have their own internal segmentation of activities.
[6] Discussion paper of the FSB on Solvent Wind-down of Derivatives and Trading Portfolios: Solvent Wind-down of Derivatives and Trading Portfolios: Discussion Paper for Public Consultation (fsb.org). The FSB is established to coordinate at the international level the work of national financial authorities and international standard-setting bodies in order to develop and promote the implementation of effective regulatory, supervisory and other financial sector policies.
[7] Under IFRS13 accounting standards, a ‘fair value hierarchy’ is used for defining the fair value of positions. Fair value measurements are categorized as level 3 of the fair value measurements are categorized as level 3 of the fair value hierarchy if the inputs are unobservable (for example due to low market activity).
On July 2nd, the European Banking Authority (EBA) published a Consultation Paper proposing amendments to its 2016 Guidelines on the application of the definition of default (DoD). As part of the
Find out moreIn an industry where growth is often measured in multiples, and value creation is expected to be both scalable and repeatable, operational excellence is no longer a supporting function—it’s
Find out moreWith extreme weather events becoming more frequent and climate policy tightening across jurisdictions, banks are under increasing pressure to understand how climate change will impact their
Find out moreWith the introduction of CRR3, effective from January 1, 2025, the ‘extra’ guarantee on Dutch mortgages – known as the Dutch National Mortgage Guarantee (NHG) – will no longer be
Find out moreAccording to the IFRS 9 standards, financial institutions are required to model probability of default (PD) using a Point-in-Time (PiT) measurement approach — a reflection of present
Find out moreInflows from open reverse repos In May 2024 the EBA stated1 that inflows from open reverse repos cannot be recognised in LCR calculations unless the call option has already been
Find out moreThis article is intended for finance, risk, and compliance professionals with business and system integration knowledge of SAP, but also includes contextual guidance for broader audiences. 1.
Find out moreOur team at Zanders has been at the forefront of implementing BACS AUDDIS (Automated Direct Debit Instruction Service) with SAP S/4HANA, helping clients to streamline their direct debit
Find out moreThailand's e-Withholding Tax (e-WHT) system officially launched on October 27, 2020, in collaboration with 11 banks, marking a significant digital transformation with far-reaching benefits for
Find out moreIn today’s rapidly evolving financial landscape, fortifying the Financial Risk Management (FRM) function remains a top priority for CFOs. Zanders has identified a growing trend among
Find out moreEmergence of Artificial Intelligence and Machine Learning The rise of ChatGPT has brought generative artificial intelligence (GenAI) into the mainstream, accelerating adoption across
Find out moreIntroduction In December 2024, FINMA published a new circular on nature-related financial (NRF) risks. Our main take-aways: NRF risks not only comprise climate-related risks,
Find out moreAs mid-sized corporations expand, enhancing their Treasury function becomes essential. International growth, exposure to multiple currencies, evolving regulatory requirements, and increased
Find out moreIndustry surveys show that FRTB may lead to a 60% increase in regulatory market risk capital requirements, placing significant pressure on banks. As regulatory market risk capital requirements
Find out moreFirst, these regions were analyzed independently such that common trends and differences could be noted within. These results were aggregated for each region such that these regions could be
Find out moreThe EU instant payments regulation1 comes into force on the 5th October this year. Importantly from a corporate perspective, it includes a VoP (verification of payee) regulation that requires
Find out moreHuman activities such as deforestation, pollution, and resource over-extraction have caused a dramatic decline in biodiversity, with approximately 1 million species at risk of extinction,
Find out moreThe evolution of the payments industry over the past 20 years has been significant, both in terms of the number of available settlement methods and how transactions can now be made. At a
Find out moreIn the ongoing efforts to enhance tax transparency for multinational corporations, tax authorities have progressively increased scrutiny on intercompany financial transactions. While the
Find out moreWith recent volatility in financial markets, firms need increasingly faster pre-trade and risk calculations to react swiftly to changing markets. Traditional computing methods for these
Find out more
In a continued effort to ensure we offer our customers the very best in knowledge and skills, Zanders has acquired Fintegral.

In a continued effort to ensure we offer our customers the very best in knowledge and skills, Zanders has acquired RiskQuest.

In a continued effort to ensure we offer our customers the very best in knowledge and skills, Zanders has acquired Optimum Prime.
You need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More Information