IFRS 17: the impact of the building blocks approach

On 18 May 2017, the International Accounting Standard Board (IASB) issued the new IFRS 17 standards. The development of these standards has been a long and thorough process with the aim of providing a single global comprehensive accounting standard for insurance contracts.
The new standards will have a significant impact on the measurement and presentation of insurance contracts in the financial statements and require significant operational changes. This article takes a closer look at the new standards, and illustrates the impact with a case study.
The standard model, as defined by IFRS 17, of measuring the value of insurance contracts is the ‘building blocks approach’. In this approach, the value of the contract is measured as the sum of the following components:
- Block 1: Sum of the future cash flows that relate directly to the fulfilment of the contractual obligations.
- Block 2: Time value of the future cash flows. The discount rates used to determine the time value reflect the characteristics of the insurance contract.
- Block 3: Risk adjustment, representing the compensation that the insurer requires for bearing the uncertainty in the amount and timing of the cash flows.
- Block 4: Contractual service margin (CSM), representing the amount available for overhead and profit on the insurance contract. The purpose of the CSM is to prevent a gain at initiation of the contract.
Risk adjustment vs risk margin
IFRS 17 does not provide full guidance on how the risk adjustment should be calculated. In theory, the compensation required by the insurer for bearing the risk of the contract would be equal to the cost of the needed capital. As most insurers within the IFRS jurisdiction capitalize based on Solvency II (SII) standards, it is likely that they will leverage on their past experience. In fact, there are many similarities between the risk adjustment and the SII risk margin.
The risk margin represents the compensation required for non-hedgeable risks by a third party that would take over the insurance liabilities. However, in practice, this is calculated using the capital models of the insurer itself. Therefore, it seems likely that the risk margin and risk adjustment will align. Differences can be expected though. For example, SII allows insurers to include operational risk in the risk margin, while this is not allowed under IFRS 17.
Liability adequacy test
Determining the impact of IFRS 17 is not straightforward: the current IFRS accounting standard leaves a lot of flexibility to determine the reserve value for insurance liabilities (one of the reasons for introducing IFRS 17). The reserve value reported under current IFRS is usually grandfathered from earlier accounting standards, such as Dutch GAAP. In general, these reserves can be defined as the present value of future benefits, where the technical interest rate and the assumptions for mortality are locked-in at pricing.
However, insurers are required to perform liability adequacy testing (LAT), where they compare the reserve values with the future cash flows calculated with ‘market consistent’ assumptions. As part of the market consistent valuation, insurers are allowed to include a compensation for bearing risk, such as the risk adjustment. Therefore, the biggest impact on the reserve value is expected from the introduction of the CSM.
The IASB has defined a hierarchy for the approach to measure the CSM at transition date. The preferred method is the ‘full retrospective application’. Under this approach, the insurer is required to measure the insurance contract as if the standard had always applied. Hence, the value of the insurance contract needs to be determined at the date of initial recognition and consecutive changes need to be determined all the way to transition date. This process is outlined in the following case study.
A case study
The impact of the new IFRS standards is analyzed for the following policy:
- The policy covers the risk that a mortgage owner deceases before the maturity of the loan. If this event occurs, the policy pays the remaining notional of the loan.
- The mortgage is issued on 31 December 2015 and has an initial notional value of € 200,000 that is amortized in 20 years. The interest percentage is set at 3 per cent.
- The policy pays an annual premium of € 150. The annual estimated costs of the policy are equal to 10 per cent of the premium.
In the case of this policy, an insurer needs to capitalize for the risk that the policy holder’s life expectancy decreases and the risk that expenses will increase (e.g. due to higher than expected inflation). We assume that the insurer applies the SII standard formula, where the total capital is the sum of the capital for the individual risk types, based on 99.5 per cent VaR approach, taking diversification into account.
The cost of capital would then be calculated as follows:
- Capital for mortality risk is based on an increase of 15 per cent of the mortality rates.
- Capital for expense risk is based on an increase of 10 per cent in expense amount combined with an increase of 1 per cent in the inflation.
- The diversification between these risk types is assumed to be 25 per cent.
- Future capital levels are assumed to be equal to the current capital levels, scaled for the decrease in outstanding policies and insurance coverage.
- The cost-of-capital rate equals 6 per cent.
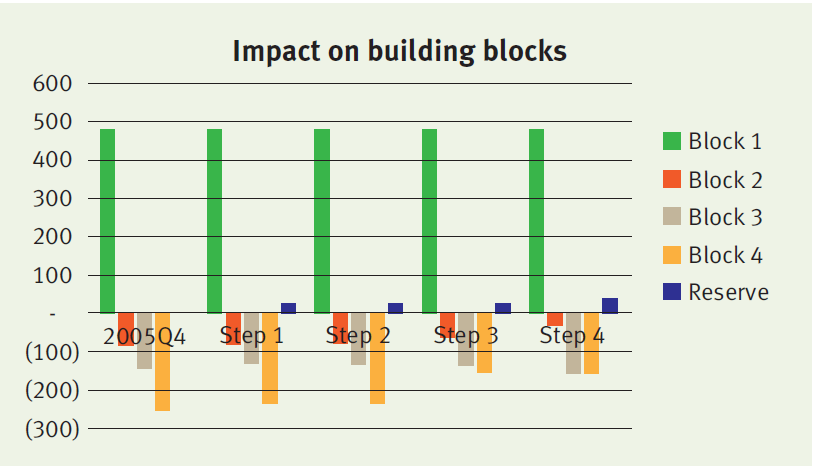
At initiation (i.e. 2015 Q4), the value of the contract under the new standards equals the sum of:
- Block 1: € 482
- Block 2: minus € 81
- Block 3: minus € 147
- Block 4: minus € 254
Consecutive changes
The insurer will measure the sum of blocks 1, 2 and 3 (which we refer to as the fulfilment cash flows) and the remaining amount of the CSM at each reporting date. The amounts typically change over time, in particular when expectations about future mortality and interest rates are updated. We distinguish four different factors that will lead to a change in the building blocks:
Step 1. Time effect
Over time, both the fulfilment cash flows and the CSM are fully amortized. The amortization profile of both components can be different, leading to a difference in the reserve value.
Step 2. Realized mortality is lower than expected
In our case study, the realized mortality is about 10 per cent lower than expected. This difference is recognized in P&L, leading to a higher profit in the first year. The effect on the fulfilment cash flows and CSM is limited. Consequently, the reserve value will remain roughly the same.
Step 3. Update of mortality assumptions
Updates of the mortality assumptions affect the fulfilment cash flows, which is simultaneously recognized in the CSM. The offset between the fulfilment cash flows and the CSM will lead to a very limited impact on the reserve value. In this case study, the update of the life table results in higher expected mortality and increased future cash outflows.
Step 4. Decrease in interest rates
Updates of the interest rate curve result in a change in the fulfilment cash flows. This change is not offset in the CSM, but is recognized in the other comprehensive income. Therefore a decrease in the discount curve will result in a significant change in the insurance liability. Our case study assumes a decrease in interest rates from 2 per cent to 1 per cent. As a result, the fulfilment cash flows increase, which is immediately reflected by an increase in the reserve value.
The impact of each step on the reserve value and underlying blocks is illustrated below.
Onwards
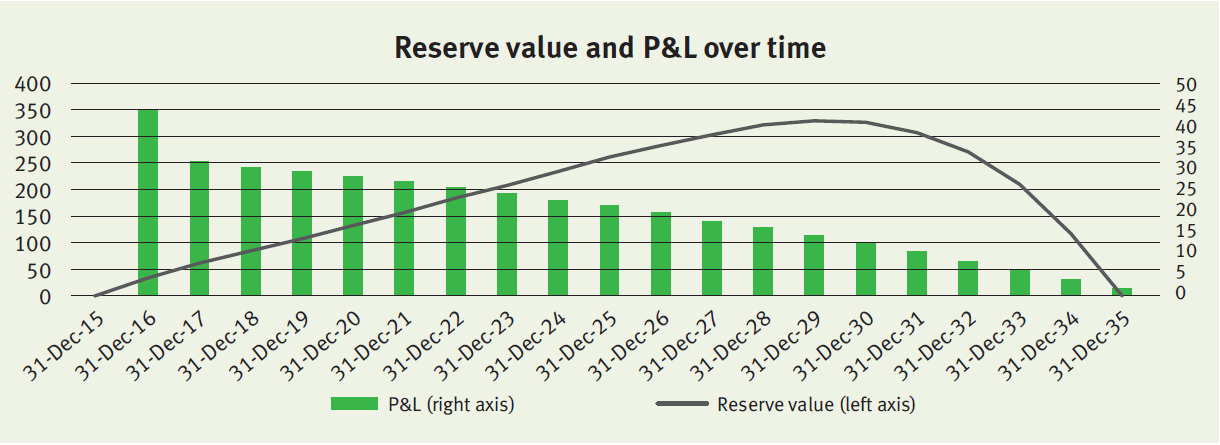
The policy will evolve over time as expected, meaning that mortality will be realized as expected and discount rates do not change anymore. The reserve value and P&L over time will evolve as illustrated below.
The profit gradually decreases over time in line with the insurance coverage (i.e. outstanding notional of the mortgage). The relatively high profit in 2016 is (mainly) the result of the realized mortality that was lower than expected (step 2 described above).
As described before, under the full retrospective application, the insurer would be required to go all the way back to the initial recognition to measure the CSM and all consecutive changes. This would require insurers to deep-dive back into their policy administration systems. This has been acknowledged by the IASB by allowing insurers to implement the standards three years after final publication. Insurers will have to undertake a huge amount of operational effort and have already started with their impact analyses. In particular, the risk adjustment seems a challenging topic that requires an understanding of the capital models of the insurer.
Zanders can support in these qualitative analyses and can rely on its past experience with the implementation of Solvency II.