
S/4 HANA Advanced Payment Management (APM) is SAP’s new solution for centralized payment hubs. Released in 2019, this solution operates as a centralized payment channel, consolidating payment flows from multiple payment sources. This article will serve to introduce its functionality and benefits.

Intraday Bank Statements offers a cash manager additional insight in estimated closing balances of external bank accounts and therefore provides the information to manage the cash more tightly on the company’s bank accounts.
Whilst over the previous years, many corporates have endeavoured to move towards a single ERP system. There are many corporates who operate in a multi-ERP landscape and will continue to do so. This is particularly the case amongst corporates who have grown rapidly, potentially through acquisitions, or that operate across different business areas. SAP’s Central Finance caters for centralized financial reporting for these multi-ERP businesses. SAP’s APM similarly caters for businesses with a range of payment sources, centralizing into a single payment channel.
SAP APM acts as a central payment processing engine, connecting with SAP Bank Communication Management and Multi-Bank Connectivity for sending of external payment Instructions. For internal payments & payments-on-behalf-of, data is fed to SAP In-House Cash. Whilst at the same time, data is transmitted to S/4 HANA Cash Management to give centralized cash forecast data.
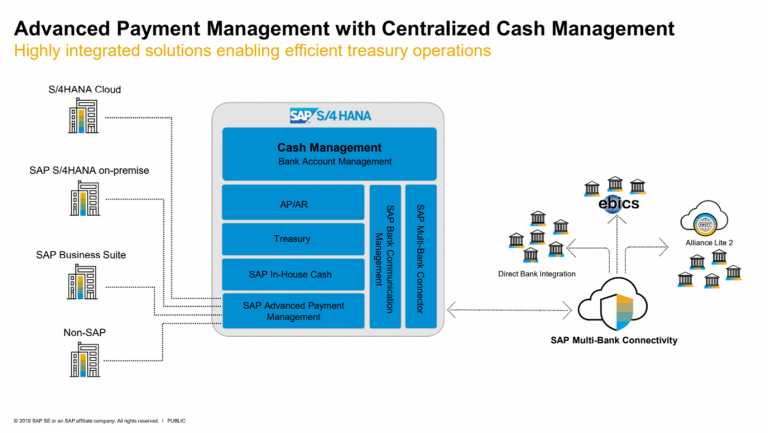
Figure 1 – SAP S/4 HANA Advanced Payment Management – Credit SAP
The framework of this product was built up as SAP Payment Engine, which is used for the processing of payment instructions at banking institutions. On this basis, it is a robust product, and will cater for the key requirements of corporate payment hubs, and much more beyond.
Building a business case
When building a business case for a centralized payment hub, it is important to look at the full range of the payment sources. This can include accounts payable/receivable (AP/AR) payments, but should also consider one-off (manual) payments, Treasury payments, as well as HR payments such as payroll. Whilst payroll is often outsourced, SAP APM can be a good opportunity to integrate payroll into a corporate’s own payment landscape (with the necessary controls of course!).
Using a centralized payment hub will help to reduce implementation time for new payment sources, which may be different ERPs. In particular, the ability of SAP APMs Input Manager to consume non-standard payment file formats helps to make this a smooth implementation process.
SAP APM applies a level of consistency across all payments and allows for a common payment control framework to be applied across the full range of payment sources.
A strength of the product is its flexible payment routing, which allows for payment routing to be adjusted according to the business need. This does not require specialist IT configuration or re-routing. It enables corporates to change their payment framework according to the need of the business, without the dependency on configuration and technology changes.
A central payment hub means no more direct bank integrations. This is particularly important for those businesses that operate in a multi-ERP environment, where the burden can be particularly heavy.
Lastly, as with most SAP products, this product benefits from native integration into modules that corporates may already be using. Payment data can be transferred directly into SAP In-House Cash using standard functionality in order to reflect intercompany positions. The richest level of data is presented to S/4 HANA Cash Management to provide accurate and up-to-date cash forecast data for Treasury front office.
Scenarios
SAP APM accommodates four different scenarios:
| Scenario | Description |
| Internal transfer | Payment from one subsidiaries internal account to the internal account of another |
| Payment on-behalf-of | Payment to external party from the internal account of a subsidiary |
| Payment in-name of | Payment to external party from the external account of a subsidiary. The derivation of the external account is performed in APM. |
| Payment in-name-of – forwarding only | Payment to external party from the external account of a subsidiary. The external account is pre-determined in the incoming payment instruction. |
A Working Example – Payment-on-behalf-of
An ERP sends a payment instruction to the APM system via iDoc. This is consumed by the input manager, creating a payment order that is ready to be processed.
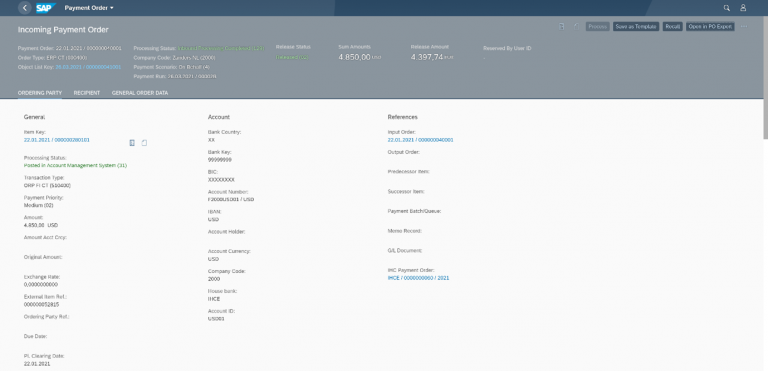
Figure 3 – Creation of Incoming Payment Order in APM
The payment order will normally be automatically processed immediately upon receipt. First the enrichment & validation checks are executed, which validate the integrity of the payment Instruction.
The payment routing is then executed for each payment item, according to the source payment data. The Payment Routing importantly selects the appropriate house bank account for payment and can be used to determine the prioritization of payments, as well as the method of clearing.
In the case of a payment-on-behalf-of, an external route will be used for the credit payment item to the third party vendor, whilst an internal route will be used to update SAP In-House Cash for the intercompany position.
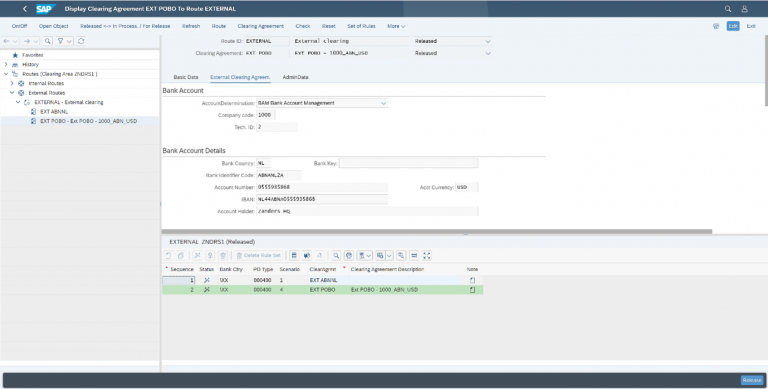
Figure 4 – Maintenance of Routes
Clearing can be executed in batches, via queues or individual processing. The internal clearing for the debit payment item must be executed into SAP In-House Cash in order to reflect the intercompany position built up. The internal clearing for the credit payment Item can be fed into the general ledger of the paying entity.
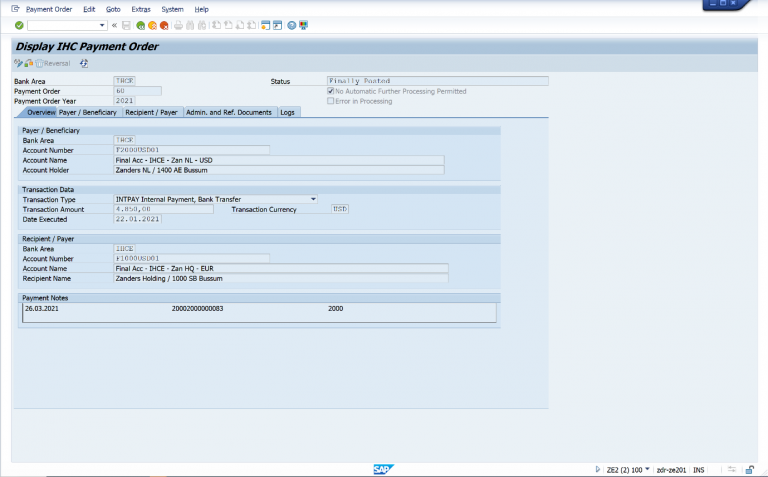
Figure 5 – Update of In-House Cash for Payment-On-Behalf or Internal Transfer Scenarios
Outgoing payment orders are created once the routing & clearing is completed. At this stage, any further enrichment & validation can be executed and the data will be delivered to the output manager. The output manager has native integration with SAP’s DMEE Payment Engine, which can be used to produce an ISO20022 payment instruction file.

Figure 6 – Payment Instruction in SAP Bank Communication Management
The outgoing payment instruction is now visible in the centralized payment status monitor in SAP Bank Communication Management.
The full processing status of the payment is visible in SAP APM, including the points of data transfer.
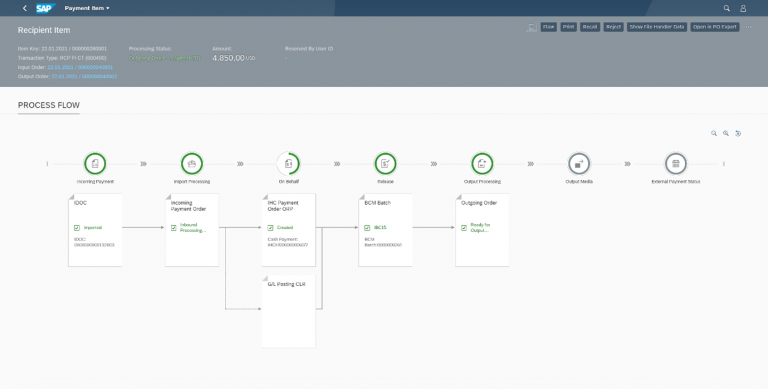
Figure 7 – SAP APM Process Flow
Introduction to Functionality
SAP APM is comprised of 4 key function areas:
- Input manager & output manager
- Enrichment and validation
- Routing
- Transaction clearing
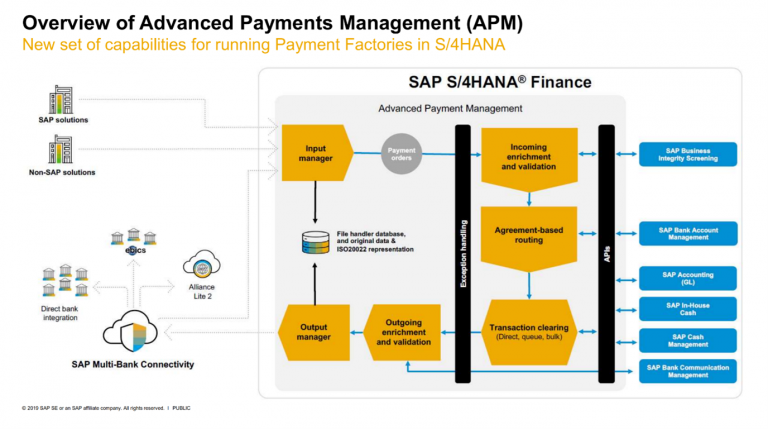
Figure 2 – SAP Advanced Payment Management Framework – Credit SAP
Input Manager
The input manager can flexibly import payment instruction data into APM. Standard converters exist for iDoc Payment Instructions (PEXR2002/PEXR2003 PAYEXT), ISO20022 (Pain.001.01.03) as well as for SWIFT MT101 messages. However, it is possible to configure new input formats that would cater for systems that may only be able to produce flat file formats.
Enrichment and Validation
Enrichment and validation can be used to perform integrity checks on payment items during the processing through APM. These checks could include checks for duplicate payment instructions. This feeds an initial set of data to S/4 HANA Cash Management (prior to routing) and can be used to return payment status messages (Pain.002) to the sending payment system.
Routing
Agreement-based routing is used to determine the selection of external accounts. This payment routing is highly flexible and permits the routing of payments according to criteria such as amounts and, beneficiary countries. The routing incorporates cut-off time logic and determines the priority of the payment as well as the sending bank account. This stage is not used for “forwarding-only” scenarios, where there is no requirement to determine the subsidiaries house bank account in the APM platform.
Clearing
Clearing involves the sending of payment data after routing to S/4 HANA Cash Management, in-house cash and onto the general ledger. According to selected route, payments can be cleared individually, or grouped into batches.
Further enrichment & validation can be performed, and external payments are routed via the output manager, which can re-use DMEE payment engines to produce payment files. These payment files can be monitored in SAP Bank Communication Management and delivered to the bank via SAP Multi-Bank Connectivity.

Traditionally the SAP Treasury functionality has been heavily focused on accounting, reporting, and monitoring of treasury transactions that have already been executed. But now, pre-trade processes can be optimized with SAP Trade Platform Integration (TPI).

In any SAP Treasury implementation, conversation will eventually turn to the integration of external systems and providers for efficient straight-through processing of data and the additional controls it provides. SAP has introduced the TPI functionality to manage one of the more challenging of these interfaces which is the integration between SAP and the external trade platforms.
The general outline for any trade integration solution would contain the following high-level components:
- The ability to collect the trade requirements in the form of FX orders from all relevant sources.
- A trade dashboard for the dealers to view and manage all requested orders.
- Ability to send the FX orders to an external trade platform for trade execution.
- Capturing of the executed trade in the treasury module, ensuring that the FX order data is also recorded to identify the purpose of the FX transaction.
There are many levels of complexity of how each of these components have been developed in the past for different organizations, from the simplest Excel templates to the most complex bespoke modules with live interfaces to manage the end-to-end trading needs.
The choice of how much an organization would want to invest in these complex solutions would depend on the volume, importance of the trading function, need for enhanced control around trading, and the level of enriched data to be recorded automatically on the deals. Now, with a standard alternative available from SAP, an extensive business case may no longer be necessary to incorporate the more complex of these requirements, as the improved controls and efficiency of processing data is available with less risk and investment than previously considered.
The solution can be broadly defined under the SAP S/4 HANA functionality and the SAP Cloud Platform (SCP) functionality as seen below.
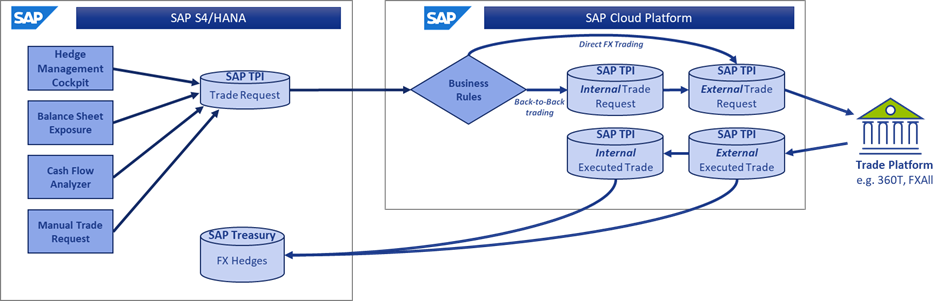
Figure 1
SAP S/4 HANA – Trade Platform Integration
The S/4 HANA functionality covers the first of the components mentioned before. Here SAP has introduced an entirely new database in the SAP environment to manage and control Trade Requests – the SAP equivalents of FX orders.
These Trade Requests may be created automatically off the back of other SAP tools such as Cash Management, Hedge Management Cockpit, Balance Sheet Hedging or simply from manual requests. The resulting Trade Request contains the same data categorizations that apply to a deal in TRM, such as portfolio, characteristics, internal references, and other fields normally found under Administration. All of this data collected prior to trading will be carried to the actual deal once executed, ensuring the dealers will not be responsible for accurately capturing this information on the deal that may not be relevant to them but necessary for further processing.
The clear benefit of this new integration is that it bridges the gap between the determination of trade requirements from Cash Management or FX risk reporting, and the dealers who are to execute and fulfil the trades. This allows the information related to the purpose of the trade (e.g.; the portfolio, exposure position, profit center, etc.) to be allocated to the Trade Request and subsequently to the executed trade automatically without the need of any manual enrichment.
Specially within the context of the Hedge Management Cockpit, this is very useful in the further automatic assignment of trades to hedge relationships, as the purpose of the trade is carried throughout the process.
SAP Cloud Platform – Trade Platform Integration
While the database in S/4 HANA remains the central transaction data source throughout the process, the functionality in SCP provides a set of tools for the dealers to manage the trades requests as needed.
This begins with some business rules to help differentiate how the trades will be fulfilled, either directly externally with a bank counterparty or internally via the treasury center.
All the external trades now can be found on the central Trade Request dashboard “Manage Trade Requests”, which acts as an order book from where the dealers/front office have a clear view on all deal requests that are been triggered from different areas of the organization and where in addition to being able to manage all the trade requests centrally, the status of each trade request is available to ensure no duplicate trading.

Figure 2
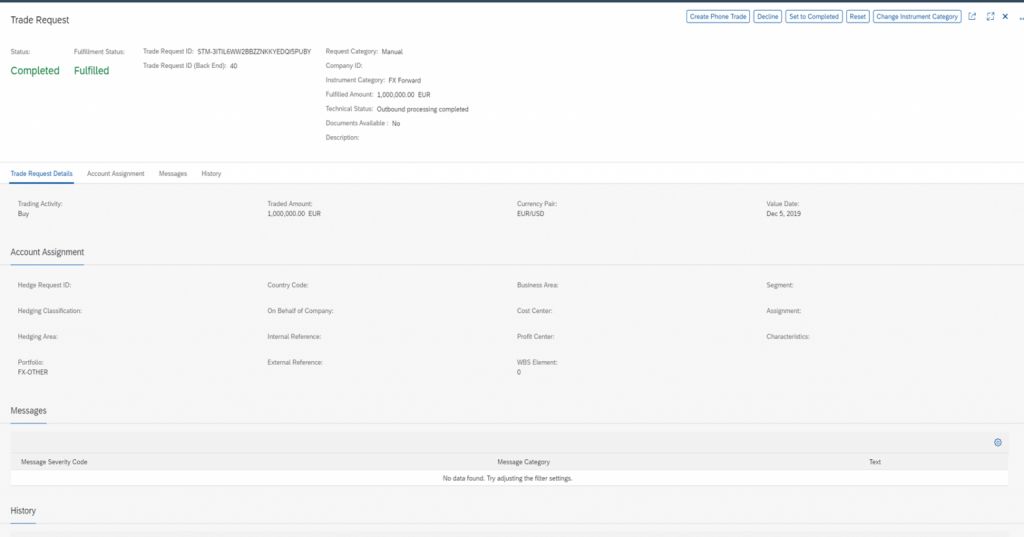
Figure 3
From the dashboard, a dealer can choose to group trades into a block, split the trades and edit them as necessary or alternatively the Trade Requests may be cancelled or manually traded as a “Phone Trade”.
The Send function on the dashboard will trigger the interface to the external trade platform for the selected trade requests taking into account the split and block trade requirements. The requests will then be executed and fulfilled on the external platform where the executed trade details such as rate and counterparty are captured back in the application, which in turns triggers the automatic creation of the FX deal in SAP S/4 HANA. The executed trade details can then be displayed on SCP application “Manage Trades”.

Figure 4
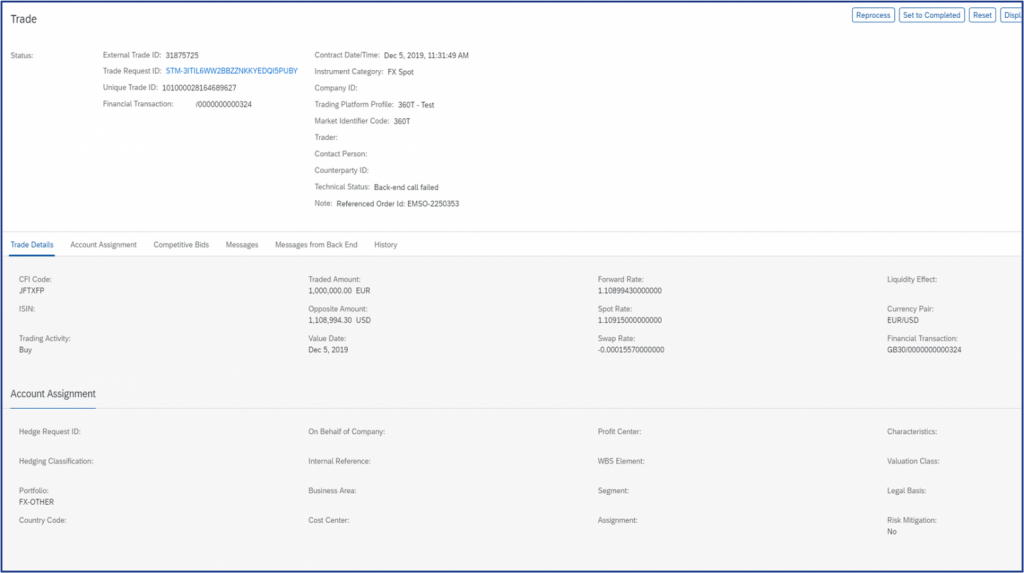
Figure 5
Internal trade requests can be automatically fulfilled at a price determined by the business rules defined by the users. This includes pricing based on the associated external deal rate (back-to-back scenario) with a commission, or pricing based on market data with a commission element.
The deals captured in SAP S/4 HANA whether internal or external, all contain the enriched data with all the originating information relating to the trade request, so that the FX deal itself accurately reflects the purpose of the position for further reporting.
Future SAP Roadmap
Although initially only the FX instruments were included in scope, SAP is now extending the ability to execute Money Market Fund purchases and sales through the platform including the associated dividend and rebate flows. This is another step to truly set up the TPI function as a central trade location for front office to operate from, covering not only FX risk requirements, but also the management of cash investment transacting.
Credit risk management is also now on the table, with pre-trade credit risk analyzer information integrated to the TPI application so that counterparty limits may be checked pre-trade to give the opportunity to exclude certain counterparties from quotation. This is certainly an improvement on the historical functionality of SAP TRM where a breach would only be noted after the deal has already been executed.
Conclusion
The recent SAP advancements in the area of TPI provide many opportunities for an organization to incorporate additional control, efficiency and transparency to the dealing process, not only for the front office, but also for the rest of the treasury team. While dealers benefit from a central platform where they can best execute the trades, middle office can get immediate feedback on their FX exposure positions as the deal immediately reflects with the correct characteristics, while the cash management team benefits from a simple ability to request and monitor the FX and investment decisions that have been sent to the dealers. The accounting team stands to benefit greatly as the accounting parameters on the deal are no longer the domain of a front office trader, but rather can be determined by the purpose of the original trade request which dictates the accounting treatment, including the automatic assignment to hedge relationships.
The SAP TPI solution therefore optimizes not only the dealers’ execution role, but also ties together the preceding and dependent processes into one fully straight through process that will benefit the whole treasury organization.

The provision of market data to support not only an organization’s treasury function but the wider business functions can become a time-consuming and potentially complex exercise.

It is no longer just about the source of market data, questions such as integration, validation, storage, consistency and distribution within an organization need to be considered. In this article we will look at some of the considerations when deciding on how to source market data and how in-built applications can reduce risk and cost while improving automation.
Which Market Data Vendor?
There are multiple market data vendors, either directly providing data or consolidating (normalizing) data from multiple sources before making it available to clients. To choose a market data vendor, an organization must firstly understand what the requirements are and this is not only based on the Treasury requirements but wider business and IT requirements:
- What data and when should it be delivered?
- IT capabilities to develop and maintain an interface or leverage inbuilt third party/core application capabilities
- Data validation and distribution
Integration
Market data vendors can provide data using multiple methods, from Excel downloads to a simple file transfer to integrated APIs to import data directly into its applications. The level of integration is driven by the market data requirements, for example, a few FX rates once a month will not justify a level of integration above importing an Excel spreadsheet or even manually entering the rates. However, most organizations require large data sets, sourced on a timely basis and validated without the need for manual intervention.
The way an organization integrates market data will, in some way, depend on the IT strategy and in-house capabilities. Some IT functions have strong in-house development teams capable of building and maintaining APIs to retrieve and import the market data, others will prefer to have the market data integration managed by a third party application. There are costs associated with both options but leveraging the inbuilt capabilities of an application that is already part of the organizations IT landscape can reduce not only the complexity of loading market data but long-term costs of maintaining the solution.
SAP and some top tier TMS applications act as a market data vendor by providing an inbuilt market data interface to access market data. SAP’s Market Rates Management module provides standard integration to both Refinitiv (formerly Thomson Reuters) as well as a more generic option for loading rates from other sources. The key benefit of SAP’s Market Rates Management is that it allows an organization to define its data requirements and import the data from a single source under a single contract while reducing the IT overhead as the module will fall under existing SAP support structures.
Validation and Distribution
Having correct and precise market data is crucial in almost every treasury process while business processes require a consistent data set across all platforms and operations. Market data validation has grown increasingly important, historically, manual, Excel-based or fully bespoke system processes have been used to validate market data, providing a very limited audit trail, introducing user errors and the potential to impact financial postings should an error not be identified. Automated data validation uses rules-based processes executed once the market data has been received that identify, remove, or flag inaccurate or anomalous information, delivering a clean dataset, ensuring the accuracy of the market data in the receiving applications/systems is correct and identical.
The distribution of validated market data to all systems and applications that require it needs to be considered when selecting a market data provider and integration solutions. There may be license implications in distributing data to multiple systems and applications which can increase the recurring costs while the options to distribute the data have the similar IT considerations as the initial integration but potentially on a larger scale, depending on how many different systems and applications require the data. As with the integration to the market data vendor, the ability to leverage 3rd party applications can reduce the costs and complexity of market data distribution.
We can support the validation and distribution process with a tool: Zanders Market Data Platform. This Zanders Inside solution, powered by Brisken, builds a bridge between the market databases and the enterprise application landscape of companies. In this way, the Market Data Platform takes away the operational risks of the market data process. The Market Data Platform runs on the SAP Cloud Platform infrastructure to ensure a secure cloud computing environment to integrate data and business processes to meet all your market data needs.
How does the Market Data Platform work?
The Market Data Platform has many functionalities. First, the platform retrieves the market data from the selected sources. Also, the platform is the source of truth for historical market data, and all activities are logged in the audit center. Subsequently calculations and market data validations are performed. Finally, the hub distributes the market data across the company’s system landscape at the right time and in the right format. The platform can directly be linked to SAP through the cloud connector, and connections to other treasury management systems are also possible, for example with IT2 or with text files. The added value of the Market Data Platform versus other solutions such as SAP Market Rates Management is the additional validation of data e.g., checking completeness and accuracy of the received data on the platform before distributing it for use.
The Zanders Market Data Platform is the solution for your market data validation processes. Would you like to learn more on this new initiative or receive a free demo of our solution? Do not hesitate to reach out to us!

Discover the significant deficiencies uncovered by the EBA’s TRIM on-site inspections and how banks must swiftly address these to ensure compliance and mitigate risk.

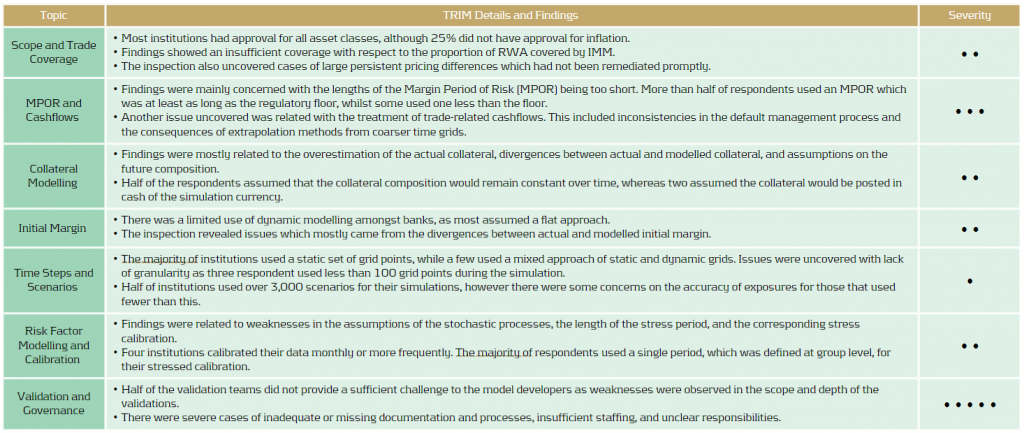
The EBA has recently published the findings and observations from their TRIM on-site inspections. A significant number of deficiencies were identified and are required to be remediated by institutions in a timely fashion.
Since the Global Financial Crisis 2007-09, concerns have been raised regarding the complexity and variability of the models used by institutions to calculate their regulatory capital requirements. The lack of transparency behind the modeling approaches made it increasingly difficult for regulators to assess whether all risks had been appropriately and consistently captured.
The TRIM project was a large-scale multi-year supervisory initiative launched by the ECB at the beginning of 2016. The project aimed to confirm the adequacy and appropriateness of approved Pillar I internal models used by Significant Institutions (SIs) in euro area countries. This ensured their compliance with regulatory requirements and aimed to harmonise supervisory practices relating to internal models.
TRIM executed 200 on-site internal model investigations across 65 SIs from over 10 different countries. Over 5,800 deficiencies were identified. Findings were defined as deficiencies which required immediate supervisory attention. They were categorised depending on the actual or potential impact on the institution’s financial situation, the levels of own funds and own funds requirements, internal governance, risk control, and management.
The findings have been followed up with 253 binding supervisory decisions which request that the SIs mitigate these shortcomings within a timely fashion. Immediate action was required for findings that were deemed to take a significant time to address.
Assessment of Market Risk
TRIM assessed the VaR/sVaR models of 31 institutions. The majority of severe findings concerned the general features of the VaR and sVaR modeling methodology, such as data quality and risk factor modeling.
19 out of 31 institutions used historical simulation, seven used Monte Carlo, and the remainder used either a parametric or mixed approach. 17 of the historical simulation institutions, and five using Monte Carlo, used full revaluation for most instruments. Most other institutions used a sensitivities-based pricing approach.
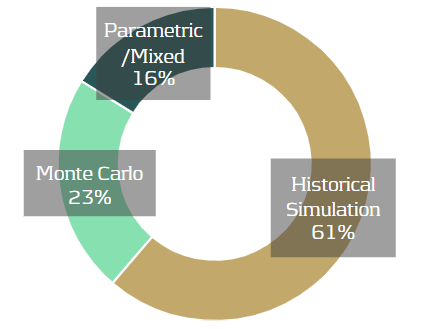
VaR/sVaR Methodology
Data: Issues with data cleansing, processing and validation were seen in many institutions and, on many occasions, data processes were poorly documented.
Risk Factors: In many cases, risk factors were missing or inadequately modelled. There was also insufficient justification or assessment of assumptions related to risk factor modeling.
Pricing: Institutions frequently had inadequate pricing methods for particular products, leading to a failure for the internal model to adequately capture all material price risks. In several cases, validation activities regarding the adequacy of pricing methods in the VaR model were insufficient or missing.
RNIME: Approximately two-thirds of the institutions had an identification process for risks not in model engines (RNIMEs). For ten of these institutions, this directly led to an RNIME add-on to the VaR or to the capital requirements.
Regulatory Backtesting
Period and Business Days: There was a lack of clear definitions of business and non-business days at most institutions. In many cases, this meant that institutions were trading on local holidays without adequate risk monitoring and without considering those days in the P&L and/or the VaR.
APL: Many institutions had no clear definition of fees, commissions or net interest income (NII), which must be excluded from the actual P&L (APL). Several institutions had issues with the treatment of fair value or other adjustments, which were either not documented, not determined correctly, or were not properly considered in the APL. Incorrect treatment of CVAs and DVAs and inconsistent treatment of the passage of time (theta) effect were also seen.
HPL: An insufficient alignment of pricing functions, market data, and parametrisation between the economic P&L (EPL) and the hypothetical P&L (HPL), as well as the inconsistent treatment of the theta effect in the HPL and the VaR, was seen in many institutions.
Internal Validation and Internal Backtesting
Methodology: In several cases, the internal backtesting methodology was considered inadequate or the levels of backtesting were not sufficient.
Hypothetical Backtesting: The required backtesting on hypothetical portfolios was either not carried or was only carried out to a very limited extent
IRC Methodology
TRIM assessed the IRC models of 17 institutions, reviewing a total of 19 IRC models. A total of 120 findings were identified and over 80% of institutions that used IRC models received at least one high-severity finding in relation to their IRC model. All institutions used a Monte Carlo simulation method, with 82% applying a weekly calculation. Most institutions obtained rates from external rating agency data. Others estimated rates from IRB models or directly from their front office function. As IRC lacks a prescriptive approach, the choice of modeling approaches between institutes exhibited a variety of modeling assumptions, as illustrated below.
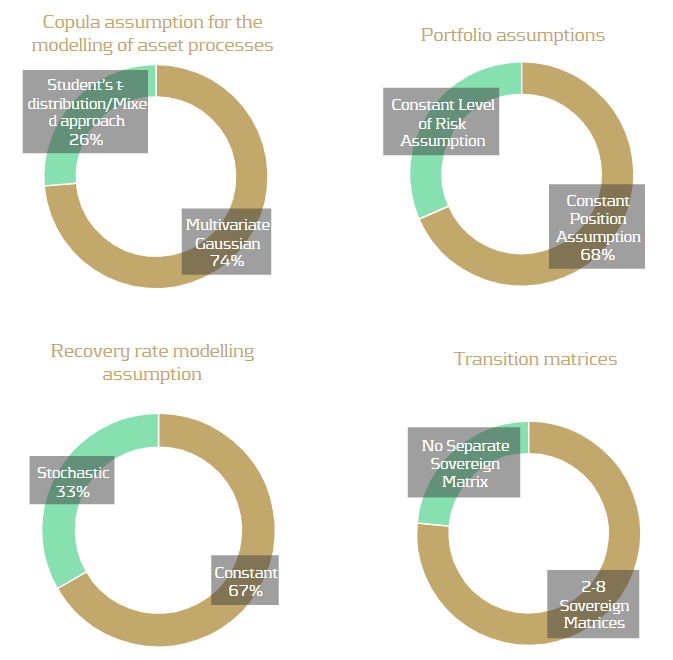
Recovery rates: The use of unjustified or inaccurate Recovery Rates (RR) and Probability of Defaults (PD) values were the cause of most findings. PDs close to or equal to zero without justification was a common issue, which typically arose for the modeling of sovereign obligors with high credit quality. 58% of models assumed PDs lower than one basis point, typically for sovereigns with very good ratings but sometimes also for corporates. The inconsistent assignment of PDs and RRs, or cases of manual assignment without a fully documented process, also contributed to common findings.
Modelingapproach: The lack of adequate modeling justifications presented many findings, including copula assumptions, risk factor choice, and correlation assumptions. Poor quality data and the lack of sufficient validation raised many findings for the correlation calibration.
Assessment of Counterparty Credit Risk
Eight banks faced on-site inspections under TRIM for counterparty credit risk. Whilst the majority of investigations resulted in findings of low materiality, there were severe weaknesses identified within validation units and overall governance frameworks.
Conclusion
Based on the findings and responses, it is clear that TRIM has successfully highlighted several shortcomings across the banks. As is often the case, many issues seem to be somewhat systemic problems which are seen in a large number of the institutions. The issues and findings have ranged from fundamental problems, such as missing risk factors, to more complicated problems related to inadequate modeling methodologies. As such, the remediation of these findings will also range from low to high effort. The SIs will need to mitigate the shortcomings in a timely fashion, with some more complicated or impactful findings potentially taking a considerable time to remediate.

The most recent S/4HANA Finance for cash management completes the bank account management (BAM) functionality with a bank account subledger concept. This final enhancement allows the Treasury team to assume full ownership in the bank account management life-cycle.

With the introduction of the new cash management in S/4HANA in 2016, SAP has announced the bank account management functionality, which treats house bank accounts as master data. With this change of design, SAP has aligned the approach with other treasury management systems on the market moving the bank account data ownership from IT to Treasury team.
But one stumbling block was left in the design: each bank account master requires a dedicated set of general ledger (G/L) accounts, on which the balances are reflected (the master account) and through which transactions are posted (clearing accounts). Very often organizations define unique GL account for each house bank account (alternatively, generic G/L accounts are sometimes used, like “USD bank account 1”), so creation of a new bank account in the system involves coordination with two other teams:
- Financial master data team – managing the chart of accounts centrally, to create the new G/L accounts
- IT support – updating the usage of the new accounts in the system settings (clearing accounts)
Due to this maintenance process dependency, even with the new BAM, the creation of a new house bank account remained a tedious and lengthy process. Therefore, many organizations still keep the house bank account management within their IT support process also on S/4HANA releases, negating the very idea of BAM as master data.
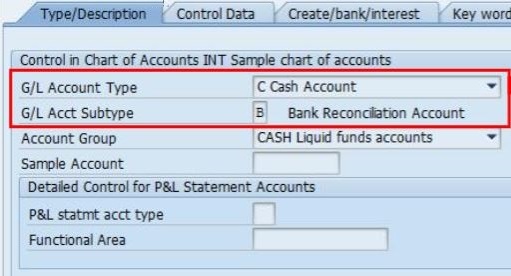
To overcome this limitation and to put all steps in the bank account management life cycle in the ownership of the treasury team completely, in the most recent S/4HANA release (2009) SAP has introduced a new G/L account type: “Cash account”. G/L accounts of this new bank reconciliation account type are used in the bank account master data in a similar way as the already established reconciliation G/L accounts are used in customer and vendor master data. However, two new specific features had to be introduced to support the new approach:
- Distinction between the Bank sub account (the master account) and the Bank reconciliation account (clearing account): this is reflected in the G/L account definition in the chart of accounts via a new attribute “G/L Account Subtype”.
- In the bank determination (transaction FBZP), the reconciliation account is not directly assigned per house bank and payment method anymore. Instead, Account symbols (automatic bank statement posting settings) can be defined as SIP (self-initiated payment) relevant and these account symbols are available for assignment to payment methods in the bank country in a new customizing activity. This design finally harmonizes the account determination between the area of automatic payments and the area of automatic bank statement processing.
In the same release, there are two other features introduced in the bank account management:
- Individual bank account can be opened or blocked for posting.
- New authorization object F_BKPF_BEB is introduced, enabling to assign bank account authorization group on the level of individual bank accounts in BAM. The user posting to the bank account has to be authorized for the respective authorisation group.
The impact of this new design on treasury process efficiency probably makes you already excited. So, what does it take to switch from the old to the new setup?
Luckily, the new approach can be activated on the level of every single bank account in the Bank account management master data, or even not used at all. Related functionalities can follow both old and new approaches side-by-side and you have time to switch the bank accounts to the new setup gradually. The G/L account type cannot be changed on a used account, therefore new G/L accounts have to be created and the balances moved in accounting on the cut-over date. However, this is necessary only for the G/L account masters. Outstanding payments do not prevent the switch, as the payment would follow the new reconciliation account logic upon activation. Specific challenges exist in the cheque payment scenario, but here SAP offers a fallback clearing scenario feature, to make sure the switch to the new design is smooth.

Implementing a hedging strategy to hedge against one common currency (the “base” currency) in SAP Treasury may be a daunting task, but in isolating and focusing on the individual building blocks required to bring this strategy to life, the challenge may not be as difficult as first anticipated.

Corporate treasuries have multiple strategic options to consider on how to manage the FX risk positions for which SAP’s standard functionality efficiently supports the activities such as balance sheet hedging and back-to-back economic hedging.
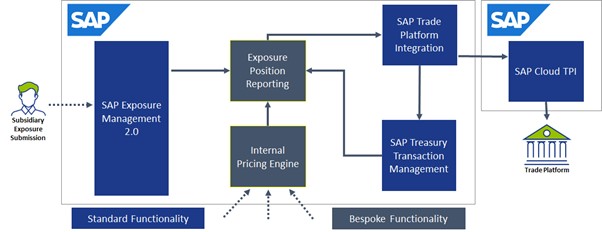
These requirements can be accommodated using applications including “Generate Balance Sheet Exposure Hedge Requests”, and the SAP Hedge Management Cockpit which efficiently joins SAP Exposure Management 2.0, Transaction Management and Hedge Accounting functionality, to create an end to end solution from exposure measurement to hedge relationship activation.
The common trait of these supported strategies is that external hedging is executed using the same currency pair as the underlying exposure currency and target currency. But this is not always the case.
Many multi-national corporations that apply a global centralized approach to FX risk management will choose to prioritize the benefits of natural offsetting of netting exposures over other considerations. One of the techniques frequently used is base currency hedging, where all FX exposures are hedged against one common currency called the “base” currency. This allows the greatest level of position netting where the total risk position is measured and aggregated according to only one dimension– per currency. The organization will then manage these individual currency risk positions as a portfolio and take necessary hedging actions against a single base currency determined by the treasury policy.
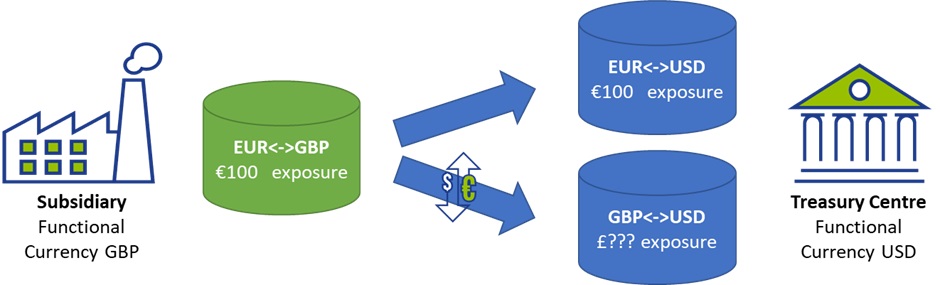
For any exposure that is submitted by a subsidiary to the Treasury Center, there are two currency risk components – the exposure currency and the target urrency. The value of the exposure currency is the “known” value, while the target currency value is “unknown”.
The immediate question that rises from this strategy is: How do we accurately record and estimate the target currency value to be hedged if the value is unknown?
To begin the journey, we first need to collect and then record the exposures into a flexible database where we can further process the data later. Experience tells us that the collection of exposures is normally done outside of SAP in a purpose-built tool, third party tool or simply an excel collection template that is interfaced to SAP. However after exposure collection, the SAP Exposure Management 2.0 functionality is capable of handling even the most advanced exposure attribute categorizations and aggregation, to form the database from which we can calculate our positions.
Importantly at this step, we need record the exposure from the perspective of the subsidiary, recording both the exposure currency and value, but also the target currency in the exposure, which at this point is unknown in value.
Internal price estimation
When we consider that for a centralized FX risk management strategy, the financial tool or contract to transfer the risk from the subsidiary to the Treasury Center is normally made through an internal FX forward or some other variation of it. At the point where both the exposure currency and target currency values are fixed according to the deal rate, we can say that it is this same rate we are to use to determine the forecasted target currency value based on the forecasted exposure currency value.
The method to find the internal dealing rate would be agreed between the subsidiary and Treasury Center and in line with the treasury policy. Examples of internal rate pricing strategies may use different sources of data with each presenting different levels of complexity:
- Spot market rates
- Budget or planning rates
- Achieved external hedge rates from recent external trading
- Other quantitative methods
Along with the question of how to calculate and determine the rate, we also need to address where this rate will be stored for easy access when estimating target currency exposure value. For most cases it may be suitable to use SAP Market Data Management tables but may also require a bespoke database table if a more complex derivation of the rate already calculated is required.
Although the complexity of the rate pricing tool may vary anywhere from picking the spot market rate on the day to calculating more complex values per subsidiary agreement, the objective remains the same – how do we calculate the rate, and where do we store this calculated rate for simple access to determine the position.
Position reporting
With exposures submitted and internal rate pricing calculated, we can now estimate our total positions for each participating currency. This entails both accessing the existing exposure data to find the exposure currency values, but also to estimate the target currency values based on the internal price estimation and fixing for each submitted exposure.
Although the hedging strategy may still vastly differ between different organizations on how they eventually cover off this risk and wish to visualize the position reports, the same fundamental inputs apply, and their hedging strategy will mostly define the layout and summarization level of the data that has already been calculated.
These layouts cannot be achieved through standard SAP reports, however by approaching the challenge as shown above, the report is simply an aggregation of the data already calculated into a preferred layout for the business users.
As a final thought, the external FX trades in place can easily be integrated into the report as well, providing more detail about the live hedged and unhedged open positions, even allowing for automatic integration of trade orders into the SAP Trade Platform Integration (TPI) to hedge the open positions, providing a controlled end to end FX risk management solution with Exposure Submission -> Trade Execution straight through processing.
SAP Trade Platform Integration (TPI)
The SAP TPI solution offers significant opportunities, not only for the base currency hedging approach, but also all other hedging strategies that would benefit from a more controlled and dynamic integration to external trade platforms. This topic deserves greater attention and will be discussed in the next edition of the SAP Treasury newsletter.
Conclusion
At first inspection, it may seem that the SAP TRM offering does not provide much assistance to implementing an efficient base currency hedging process. However, when we focus on these individual requirements listed above, we see that a robust solution can be built with highly effective straight through processing, while still benefiting from largely standard SAP capability.
The key is the knowledge of how these building blocks and foundations of the SAP TRM module can be used most effectively with the bespoke developments on internal pricing calculations and position reporting layouts to create a seamless integration between standard and bespoke activities.

At Inmarsat, intercompany netting is gross amount based and settled via their SAP In-House bank solution, however, the current setup made intercompany reconciliation difficult and intercompany funding needs less transparent. We offered a solution.

Inmarsat had one FTE spending 3-4 hours every month, including during the month-end close, manually allocating an excessive number of payments against open invoices on the customer ledger. This was time that should have been spent on value-add activities that could have resulted in closing the books earlier. How did this come about?
In the current setup, credit/debit balances are building up on multiple intercompany payables/receivables accounts with the same entity, reflecting various business transactions (intercompany invoicing, cash concentration, POBO payments, intercompany settlement). This situation makes intercompany reconciliation more difficult and intercompany funding needs, less transparent.
Searching the solution
As part of the Zanders Treasury Technology Support contract, Inmarsat asked Zanders to define and implement a solution, which would reduce the build-up of multiple intercompany receivables/payables from cash concentration, and instead, reflect these movements in the in-house bank accounts of the respective entity.
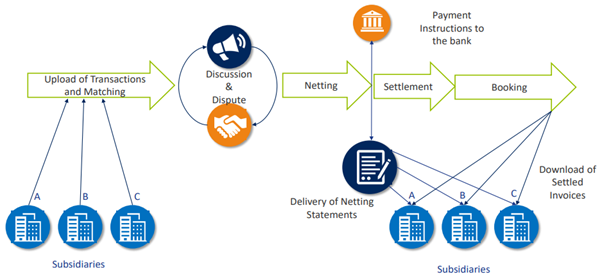
During the initial set-up of in-house cash (IHC), it was our understanding that all intercompany netting inflows should auto-match with open invoices, if both the Vendor and customer invoices carried the same reference. “Netting” in Inmarsat terms means a settlement of intercompany customer/vendor invoices through IHC.
Unfortunately, a very small percentage of IHC intercompany inflows auto-matched with open customer invoices (14% achieved in May 2020). Sample cases reviewed show that the automatic matching was happening where references on both vendor and customer invoices are same. However, for most cases, even where references were the same, no auto-matching happened.
The IHC Inter-Co Netting issue
In phase 1, the intercompany netting issues were addressed. Intercompany netting is an arrangement among subsidiaries in a corporate group where each subsidiary makes payments to, or receives payment from, a clearing house (Netting Centre) for net obligations due from other subsidiaries in the group. This procedure is used to reduce credit/settlement risk. Also known as multilateral netting, netting and multilateral settlement.
SAP standard system logic/process:
FINSTA Bank statements are internal bank statements for internal Inhouse Cash Accounts and these statements post to the GL and subledger of the participating company codes, so that the inhouse cash transactions are reflected in the Balance Sheet.
Requirement:
Any Intercompany transactions posted through the FINSTA bank statements, should be able to correctly identify the open items on the Accounts Receivable (AR) side to post and clear the correct line items.
Root Cause Analysis:
We found that a payment advice segment present in FINSTA was overriding the clearing information found as per interpretation algorithm ‘021’. As such this was forcing the system to rely on the information in the payment advice notes to find a clearing criterion.
The documents should be cleared based on the information passed to the payment notes table FEBRE.
As a solution, we set the variable DELETE_ADVICE with an ‘X’ value in user exit EXIT_SAPLIEDP_203, so that SAP relied on the interpretation algorithm via a search on the FEBRE table and not the payment advice, for identifying the documents uniquely, and then clearing them. Information from the FEBRE table that includes the document reference, feeds into the interpretation algorithm to uniquely identify the AR open item to clear. This information is passed on to table FEBCL that has the criteria to be used for clearing.
With the above change maintained, SAP will always use the interpretation algorithm maintained in the posting rule for deriving the open items.
Prior to the fix, the highest percentage auto-match for 2020 was 16%. Post fix, we increased the automatch to 85%.

Table 1: interpretation algorithm
Client’s testimonial
Christopher Killick, ERP Functional Consultant at Inmarsat, expressed his gratitude for the solution offered by our Treasury Technology Support services in a testimonial:
“In the autumn of 2019, Inmarsat was preparing for takeover by private equity. At the same time, our specialized treasury resources were stretched. Fortunately, Zanders stepped in to ensure that the myriad of complex changes required were in place on time.
- Make a number of general configuration improvements to our treasury management and in-house cash setup.
- Educate us on deal management and business partner maintenance.
- Update and vastly improve our Treasury Management User Guide.
- Run a series of educational and analytical workshops.
- Map out several future improvements that would be of great benefit to Inmarsat – some of which have now been implemented.
- Without this support it is likely that Inmarsat would no longer be using SAP TRM.
Inmarsat’s relationship with Zanders has continued through a Treasury Technology Support Contract, that is administered with the utmost professionalism and care. In the past six months or so, a large number of changes have been implemented. Most of these have been highly complex, requiring real expertise and this is where the true benefit of having an expert treasury service provider makes all the difference.”
Conclusions
Since the start of the TTS support contract, Zanders has been intimately engaged with Inmarsat to help support and provide expert guidance with usage and continuous improvement of the SAP solution. This is just a small step in optimising the inter-company netting, but a big steps towards automation of the core IHB processes.
If you want to know more about optimising in-house bank structures or inter-company netting then please get in contact with Warren Epstein.

A successful SAP implementation or SAP enhancement requires a successful data migration. There are numerous ways to organize an effective data transfer, even to the point where it is quite hard to navigate amongst them. One way to simplify the choice is to use the standard solutions provided by SAP itself. This approach has a few advantages, however, also has its limitations.

Because of these limitations, many implementation partners develop their custom in-house solutions to address the requirements of their clients. SAP is constantly working on improving its standard tools, through updates, and new functionalities. This article provides insight into SAP’s standard data migration tools as well as Zanders’ approach and tools, which successfully help our clients with the migration of treasury data.
Data migration objects: master and transactional
Data migration is the process of transferring data from a source (e.g. a legacy system or other type of data storage) to the target system – SAP. However, data migration is not simply a ‘lift and shift’ exercise, the data must also be transformed and made complete in order to efficiently facilitate the required business operations in the new system.
Since the vast majority of business processes can be supported via SAP, the variety of master data objects that are required becomes extremely large. SAP SCM (Supply Chain Management) module necessitates, for example, information about the materials, production sequencing or routing schedules while HCM (human capital management) requires data regarding employees and organizational structure. This article will focus in detail on the TRM (treasury and risk management) module and the typical master data objects that are required for its successful operation.
Core Treasury related Master data objects include but not limited to:
Business Partners:
Business Partner data contains information about the trading counterparties a corporate operates a business with. This data is very diverse and includes everything starting from names, addresses and bank accounts to types of approved transactions and currencies they should take place in. The business partner data is structured in a specific way. There are several concepts which should be defined and populated with data:
- Business Partner Category: defines what kind of party the business partner (private individual, subsidiary, external organization, etc.) is and basic information such as name and address
- Business Partner Role: defines the business classification of a business partner (Employee”, “Ordering Party” or “Counterparty”). This determines which kinds of transactions can occur with this business partner.
- Business Partner Relationship: This represents the relationship between two business partners.
- Business Partner Group Hierarchy: The structure of a complex organization with many subsidiaries or office geographies can be defined here.
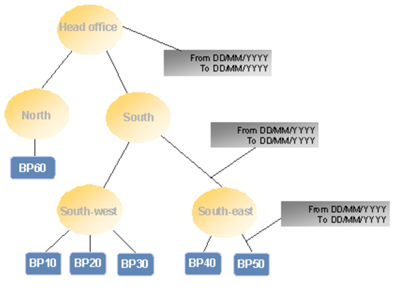
Figure 1: the organizational structure of a company with various branches, according to the region to which they belong. Source: SAP Help Portal
House bank accounts:
This master data object contains information regarding the bank accounts at the house banks. It consists of both basic information such as addresses, phone numbers and bank account numbers, as well as more complicated information, such as the assignment of which bank account should be used for transactions within certain currencies.
In-house cash (IHC):
IHC data includes:
- Bank accounts
- Conditions: interest, limits etc.
Another important part of data migration is transactional data, which includes Financial transactions (deals), FX exposure figures etc.
Financial transactions:
Transactional data includes active and expired deals, which have been booked in the legacy system. The migration of such data may also require consolidation of information from several sources and its enhancement meanwhile maintaining its accuracy during the transfer. The amount of data is usually very large, adding another layer of complexity to the migration of this master data object.
The above examples of the master and transactional data objects relevant to SAP TRM give an insight into the complexity and volume of data required for a full and successful data migration. To execute such a task, there are a few approaches that can be utilized, which are supported by the data migration solutions discussed below.
Legacy Data migration solutions
At Zanders, we may propose different solutions for data migration, which are heavily dependent on a client specific characteristics. The following factors are taken into account:
- Specificity of the data migration object (complexity, scope)
- Type and quantity of legacy and target systems (SAP R/3, ECC, HANA, non-SAP, Cloud or on premise etc.)
- Frequency to which the migration solution is to be used (one off or multiple times)
- The solution ownership (IT support or Business)
After analysis of the above factors, the following SAP standard solutions from the below list may be proposed.
SAP GUI Scripting: is an interface to SAP for Windows and Java. Users can automate manual tasks through recording scripts per a specific manual process, and with a complete and correct dataset, the script will create the data objects for you. Scripting is usually used to support the business with different parts of the data migration or enhancement and is often developed and supported in-house for micro and recurrent migration activities.
SAP LSMW (Legacy System Migration Workbench) was a standard SAP data upload solution used in SAP ECC. It allowed the import of data, its required conversion and its export to the target SAP system. LSMW supports both batch and direct input methods. The former required the data to be formatted in a standardized way and stored in a file. This data was then uploaded automatically, with the downside of following a regular process involving transaction codes and processing screens. The latter required the use of an ABAP program, which uploads the data directly into the relevant data tables, omitting the need of transaction codes and processing screens seen in batch input methods.
SAP S/4 HANA Migration cockpit is a recommended standard data migration tool for SAP S/4 HANA. With this new iteration the tool became much more user friendly and simple to use. It supports the following migration approaches:
- Transfer data using files: SAP provides templates for the relevant objects.
- Transfer data using staging tables. Staging tables are created automatically in SAP HANA DB schema. Populate the tables with the business data and load into SAP S/4 HANA.
- Transfer data directly from SAP ERP system to SAP S/4 HANA (new feature from SAP S/4 Hana 1909)
- extra option available from HANA 2020 -> Migrate data using Staging tables which can be pre-populated using with XML templates or SAP / third party ETL (extract, transfer, load) tools.
From HANA 2020 SAP enhances the solution with:
- One harmonized application in Fiori
- Transport concept. The data can be released between SAP clients and systems
- Copying of the migration projects
SAP provides a flexible solution to integrate custom objects and enhancements for data migration via the Migration object modeler.
SAP migration cockpit has a proper set of templates to migrate Treasury deals. Currently SAP supports the following financial transaction types: Guarantees, Cap/Floor, CPs, Deposit at notice, Facilities, Fixed Term Deposits, FX, FX options, Interest Rate Instrument, IRS, LC, Security Bonds, Security Class, Stock.
Standard SAP tools are relatively competent solutions for data migration, however due to the complexity and scope of TRM related master data objects, they prove to not be sophisticated enough for certain clients. For example, they do support basic business partner setup. However, for most clients the functionality to migrate complex business partner data is required. In many cases, implementation partners, including Zanders, develop their own in-house solutions to tackle various TRM master data migration issues.
Zanders pre-developed solution – BP upload tool
Within SAP Treasury and Risk management, the business partner plays an important role in the administration. Unfortunately, with all new SAP installations it is not possible to perform a mass and full creation of the current business partners with the data required for Treasury.
SAP standard tools require enhancements to accommodate for the migration of the required data of Business partners, especially their creation and assignment of finance specific attributes and dependencies, which requires substantial time-consuming effort when performed manually.
Zanders acknowledges this issue and has developed a custom tool to mass create business partners within SAP. Our solution can be adjusted to different versions of SAP: from ECC to S/4 HANA 2020.
The tool consists of:
- Excel pre-defined template with a few tabs which represent different part of the BP master data: Name, Address, Bank data, Payment instructions, Authorizations etc.
- Custom program which can perform three actions: Create basic data for BP, enhance/amend or delete existing BPs in SAP.
- Test and production runs are supported with the full application log available during the run. The log will show if there is any error in the BP creation.
The migration of the master and transaction data is a complex but vital process for any SAP implementation project. This being said, the migration of the data (from planning to realization) should be viewed as a separate deliverable within a project.
Zanders has unique experience with Treasury data transformation and migration, and we are keen to assist our clients in selecting the best migration approach and the best-fit migration tool available from SAP standard. We are also able assist clients in the development of their own in-house solution, if required.
Should you have any questions, queries or interest in SAP projects please contact Aleksei Abakumov or Ilya Seryshev.

Discover how leveraging synergies across key regulatory frameworks like SIMM, BCBS 239, SA-CVA, and the IBOR transition can streamline your compliance efforts and ease the burden of FRTB implementation.

Regulatory Landscape
Despite a delay of one year, many banks are struggling to be ready for FRTB in January 2023. Alongside the FRTB timeline, banks are also preparing for other important regulatory requirements and deadlines which share commonalities in implementation. We introduce several of these below.
SIMM
Initial Margin (IM) is the value of collateral required to open a position with a bank, exchange or broker. The Standard Initial Margin Model (SIMM), published by ISDA, sets a market standard for calculating IMs. SIMM provides margin requirements for financial firms when trading non-centrally cleared derivatives.
BCBS 239
BCBS 239, published by the Basel Committee on Banking Supervision, aims to enhance banks’ risk data aggregation capabilities and internal risk reporting practices. It focuses on areas such as data governance, accuracy, completeness and timeliness. The standard outlines 14 principles, although their high-level nature means that they are open to interpretation.
SA-CVA
Credit Valuation Adjustment (CVA) is a type of value adjustment and represents the market value of the counterparty credit risk for a transaction. FRTB splits CVA into two main approaches: BA-CVA, for smaller banks with less sophisticated trading activities, and SA-CVA, for larger banks with designated CVA risk management desks.
IBOR
Interbank Offered Rates (IBORs) are benchmark reference interest rates. As they have been subject to manipulation and due to a lack of liquidity, IBORs are being replaced by Alternative Reference Rates (ARRs). Unlike IBORs, ARRs are based on real transactions on liquid markets rather than subjective estimates.
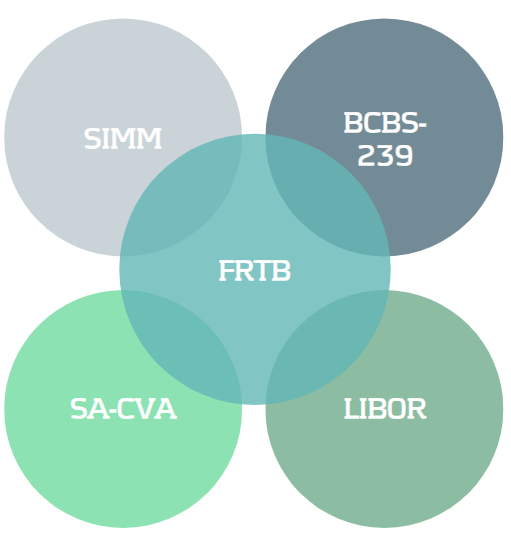
Synergies With Current Regulation
Existing SIMM and BCBS 239 frameworks and processes can be readily leveraged to reduce efforts in implementing FRTB frameworks.
SIMM
The overarching process of SIMM is very similar to the FRTB Sensitivities-based Method (SbM), including the identification of risk factors, calculation of sensitivities and aggregation of results. The outputs of SbM and SIMM are both based on delta, vega and curvature sensitivities. SIMM and FRTB both share four risk classes (IR, FX, EQ, and CM). However, in SIMM, credit is split across two risk classes (qualifying and non-qualifying), whereas it is split across three in FRTB (non-securitisation, securitisation and correlation trading). For both SbM and SIMM, banks should be able to decompose indices into their individual constituents.
We recommend that banks leverage the existing sensitivities infrastructure from SIMM for SbM calculations, use a shared risk factor mapping methodology between SIMM and FRTB when there is considerable alignment in risk classes, and utilise a common index look-through procedure for both SIMM and SbM index decompositions.
BCBS 239
BCBS 239 requires banks to review IT infrastructure, governance, data quality, aggregation policies and procedures. A similar review will be required in order to comply with the data standards of FRTB. The BCBS 239 principles are now in “Annex D” of the FRTB document, clearly showing the synergy between the two regulations. The quality, transparency, volume and consistency of data are important for both BCBS 239 and FRTB. Improving these factors allow banks to easily follow the BCBS 239 principles and decrease the capital charges of non-modellable risk factors. BCBS 239 principles, such as data completeness and timeliness, are also necessary for passing P&L attribution (PLA) under FRTB.
We recommend that banks use BCBS 239 principles when designing the necessary data frameworks for the FRTB Risk Factor Eligibility Test (RFET), support FRTB traceability requirements and supervisory approvals with existing BCBS 239 data lineage documentation, and produce market risk reporting for FRTB using the risk reporting infrastructure detailed in BCBS 239.
Synergies With Future Regulation
The IBOR transition and SA-CVA will become effective from 2023. Aligning the timelines and exploiting the similarities between FRTB, SA-CVA and the IBOR transition will support banks to be ready for all three regulatory deadlines.
SA-CVA
Four of the six risk classes in SA-CVA (IR, FX, EQ, and CM) are identical to those in SbM. SA-CVA, however, uses a reduced granularity for risk factors compared to SbM. The SA-CVA capital calculation uses a similar methodology to SbM by combining sensitivities with risk weights. SA-CVA also incorporates the same trade population and metadata as SbM. SA-CVA capital requirements must be calculated and reported to the supervisor at the same monthly frequency as for the market risk standardised approach.
We recommend that banks combine SA-CVA and SbM risk factor bucketing tasks in a common methodology to reduce overall effort, isolate common components of both models as a feeder model, allowing a single stream for model development and validation, and develop a single system architecture which can be configured for either SbM or SA-CVA.
IBOR Transition
Although not a direct synergy, the transition from IBORs will have a direct impact to the Internal Models Approach (IMA) for FRTB and eligibility of risk factors. As the use of IBORs are discontinued, banks may observe a reduction in the number of real-price observations for associated risk factors due to a reduction in market liquidity. It is not certain if these liquidity issues fall under the RFET exemptions for systemic circumstances, which apply to modellable risk factors which can no longer pass the test. It may be difficult for banks to obtain stress-period data for ARRs, which could lead to substantial efforts to produce and justify proxies. The transition may cause modifications to trading desk structure, the integration of external data providers, and enhanced operational requirements, which can all affect FRTB.
We recommend that banks investigate how much data is available for ARRs, for both stress-period calculations and real-price observations, develop any necessary proxies which will be needed to overcome data availability issues, as soon as possible, and Calculate IBOR capital consequences through the existing FRTB engine.
Conclusion
FRTB implementation is proving to be a considerable workload for banks, especially those considering opting for the IMA. Several FRTB requirements, such as PLA and RFET, are completely new requirements for banks. As we have shown in this article, there are several other important regulatory requirements which banks are currently working towards. As such, we recommend that banks should leverage the synergies which are seen across this regulatory landscape to reduce the complexity and workload of FRTB.

If you want to go fast, go alone. If you want to go far, go together

At the birth of any project, it is crucial to determine the most suitable project management framework by which the treasury objectives can be achieved. Whether the focus is on TMS implementation, treasury transformation or risk management, the grand challenge remains – to ensure the highest quality of the delivered outcome while understanding the realistic timelines and resources. In this article we shed a light on the implications of project management methodologies and address its main concepts and viewpoints, accompanied by experiences from past treasury projects.
In recent years, big corporates have been strategically cherry-picking elements from various methodologies, as there is no one-size-fits-all. At Zanders, our treasury project experience has given us an in-depth knowledge in this area. Based on this knowledge, and depending on several variables – project complexity, resource maturity, culture, and scope – we advise our clients on the best project management methodology to apply to a specific treasury project.
We have observed that when it comes to choosing the project management methodology for a new treasury project, most corporates tend to choose what is applied internally or on previous projects. This leverages the internal skillsets and maturity around that framework. But is this really the right way to choose?
Shifting from traditional methodologies
As the environment that businesses operate in is undergoing a rapid and profound change, the applicability and relevance of the traditional project management methodologies have been called in to question. In the spirit of becoming responsive to unforeseen events, companies sensed the urgency to seek methods that are geared to rapid delivery and with the ability to respond to change quickly.
Embracing agile
The agile management framework aims to enhance project delivery by maximizing team productivity, while minimizing the waste inherent in redundant meetings, repetitive planning or excessive documentation. Unlike the traditional command and control-style management, which follows a linear approach, the core of agile methodology lies in a continuous reaction to a change rather than following a fixed plan.
This type of framework is mostly applied in an environment where the problem to be solved is complex, its solution is non-linear as it has many unknowns, and the project requirements will most likely change during the lifetime of the project as the target is on a constant move.
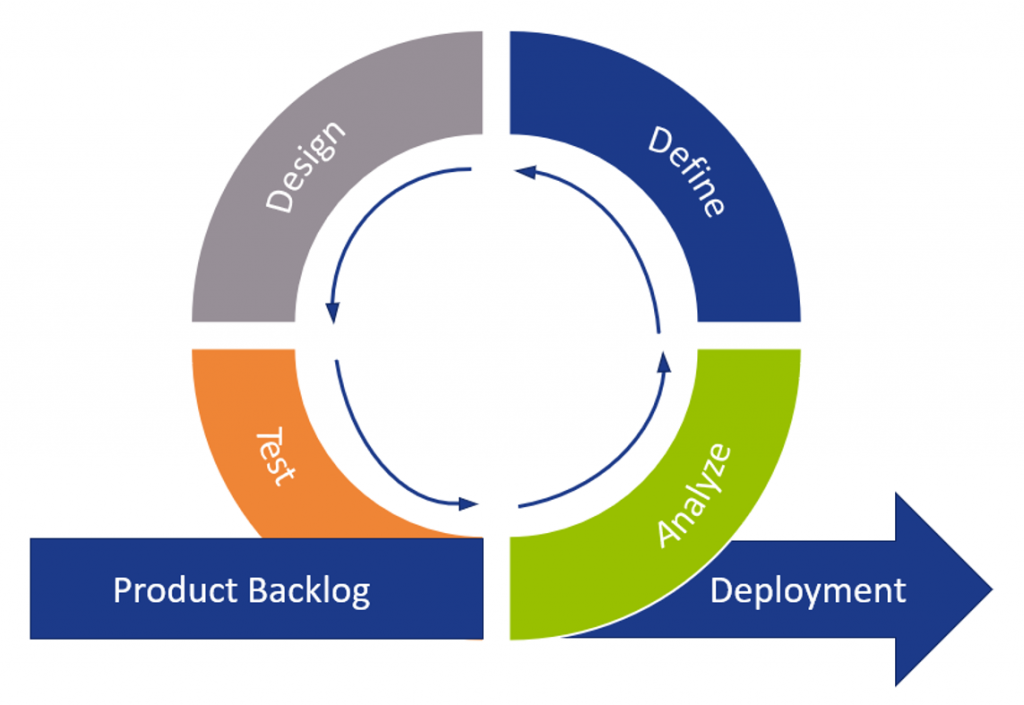
The illustration of an agile process (figured above) portrays certain similarities to the waterfall approach, in the sense of breaking the entire project in to several phases. However, while these phases in the waterfall approach are sequential, the activities in agile methodology can be run in parallel.
Agile principles promote changing requirements and sustainable development, and deliver working software frequently which can add value sooner. However, from a treasury perspective, you often cannot go live in pieces/functionalities since it increases risk or, when a requirement comes late in process, teams might not have the resources or availability to support the new requirement, creating delivery risk.
Evolving Agile and its forms
Having described the key principles of agile methodology, it is vital to state that over the years it has become a rather broad umbrella-term that covers various concepts that abide by the main agile values and principles.
One of the most popular agile forms is the Kanban approach, the uniqueness of which lies in the visualization of the workflow by building a so-called (digital) Kanban board. Scrum is another project management framework that can be used to manage iterative and incremental projects of all types. The Product Owner works with the team to identify and prioritize system functionality by creating a Product Backlog, with an estimation of software delivery by the functional teams. Once a Sprint has been delivered, the Product Backlog is analyzed and reprioritized, and the next set of deliverables is selected for the next Sprint. Lean framework focuses on delivering value to the customer through effective value-added analysis. Lean development eliminates waste by asking users to select only the truly valuable features for a system, prioritize the features selected, and then work on delivering them in small batches.
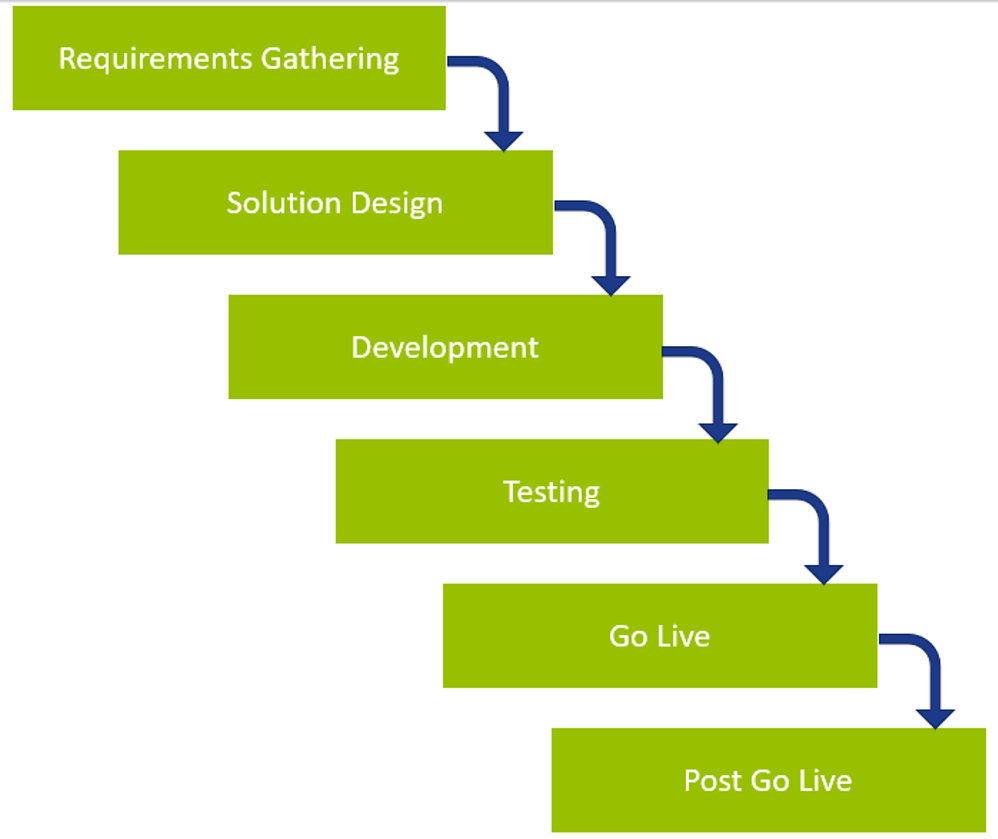
Waterfall methodologies – old but good
Even though agile methodologies are now widely accepted and rising in popularity, certain types of projects benefit from highly planned and predictive frameworks. The core of this management style lies in its sequential design process, meaning that an upcoming phase cannot begin until the previous one is formally closed. Waterfall methodologies are characterized by a high level of governance, where documentation plays a crucial role. This makes it easier to track the progress and manage the project scope in general. Projects that highly benefit from this methodology are characterized by their ability to define the fixed-end requirements up-front and are relatively smaller in size. For a project to move to the next phase, all current documentation must be approved by all the involved project managers. The excessive documentation ensures that the team members are familiar with the requirements of the coming phase.
Depending on the scope of the project, this progressive method breaks down the workload into several discrete steps, as shown here:
Project Team Structures
There are also differences between the project structures and the roles used in the two presented frameworks.
In waterfall, the common roles – outside of delivery or the functional team – to support and monitor the project plan are the project managers (depending on the size of the project there can be one or many, creating a project management office (PMO) structure) and a program director. In agile, the role structure is more intricate and complex. Again, this depends on the size of the treasury project.
As stated previously, agile project management relies heavily on collaborative processes. In this sense, a project manager is not required to have a central control, but rather appointing the right people to right tasks, increasing cross-functional collaboration, and removing impediments to progress. The main roles differ from the waterfall approach and can be labelled as Scrum master, Agile coach and Product owner.
Whatever the chosen approach is for a treasury project, one structure is normally seen in both – the steering committee. In more complex and bigger treasury projects (with greater impact and risk to the organization) sometimes a second structure or layer on top of the steering committee (called governance board) is needed. The objective of each one differs.
The Project Steering Committee is a decision-making structure within the project governance structure that consists of top managers (for example, the leads of each treasury area involved directly in the project) and decision makers who provide strategic direction and policy guidance to the project team and other stakeholders. They also:
- Monitor progress against the project management plan.
- Define, review and monitor value delivered to the business and business case.
- Review and approve changes made to project resource plan, schedules, and scope. This normally depends on the materiality of the changes.
- Review and approve project deliverables.
- Resolve conflicts between stakeholders.
The Governance Board, when needed, is more strategical by nature. For example, in treasury projects they are normally represented by the treasurer, CFO, and CEO. Some of the responsibilities are to:
- Monitor and help unblock major risks and potential project challenges.
- Keep updated and understand broader impacts coming out from the project delivery.
- Provide insights and solutions around external factors that might impact the treasury project (e.g. business strategic changes, regulatory frameworks, resourcing changes).
Other structures might be needed to be designed or implemented to support project delivery. More focused groups require different knowledge and expertise. Again, no one solution fits all and it depends on the scope and complexity of the treasury project.
The key decision factors that should be considered when selecting the project structure are:
Roles and responsibilities: Clearly define all roles and responsibilities for each project structure. That will drive planning and will clearly define who should do what. A lack of clarity will create project risks.
Size and expertise: Based on roles and responsibilities, and using a clear RAPID or RACI matrix, define the composition of these structures. There should not be a lot of overlap in terms of people in the structure. In most cases ‘less is more’ if expertise and experience is ensured.
The treasury project scope, complexity and deliverables should drive these structures. Like in the organizational structure of a company, a project should follow the same principles. A pyramid structure should be applied (not an inverted one) in which the functional (hands-on) team should be bigger than other structures.
Is a hybrid model desirable? Our conclusion
While it is known that all methodologies ultimately accomplish the same goal, choosing the most suitable framework is a critical success factor as it determines how the objectives are accomplished. Nowadays, we see that a lot of organizations are embracing a hybrid approach instead of putting all their hopes into one method.
Depending on the circumstances of the treasury project, you might find yourself in a situation where you employ the waterfall approach at the very beginning of the project. This creates a better structure for planning, ensures a common understanding of the project objectives and creates a reasonable timeline of the project. When it comes to the execution of the project, however, it becomes apparent that there needs to be space for some flexibility and early business engagement, as the project happens to be in a dynamic environment. Hence, it becomes beneficial to leverage an agile approach. Such project adapts a “structured agile” methodology, where the planning is done in the traditional way of management, while the execution implements some agile articles.


